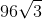SAT Math : Basic Squaring / Square Roots
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #2 : How To Divide Square Roots
Simplify:
When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.
Let's simplify this even further by factoring out a 
Example Question #23 : Square Roots And Operations
Simplify:
When dividing square roots, we divide the numbers inside the radical. Simplify if necessary.
Let's simplify this even further by factoring out a 
Example Question #31 : Basic Squaring / Square Roots
Simplify
9 ÷ √3
2
3
3√3
not possible
none of these
3√3
in order to simplify a square root on the bottom, multiply top and bottom by the root
Example Question #101 : Arithmetic
Simplify:
√112
12
10√12
20
4√7
4√10
4√7
√112 = {√2 * √56} = {√2 * √2 * √28} = {2√28} = {2√4 * √7} = 4√7
Example Question #31 : Basic Squaring / Square Roots
Simplify:
√192
√192 = √2 X √96
√96 = √2 X √48
√48 = √4 X√12
√12 = √4 X √3
√192 = √(2X2X4X4) X √3
= √4X√4X√4 X √3
= 8√3
Example Question #1 : How To Simplify Square Roots
What is the simplest way to express 
First we will list the factors of 3888:
Example Question #31 : Basic Squaring / Square Roots
Simplify:
4√27 + 16√75 +3√12 =
4*(√3)*(√9) + 16*(√3)*(√25) +3*(√3)*(√4) =
4*(√3)*(3) + 16*(√3)*(5) + 3*(√3)*(2) =
12√3 + 80√3 +6√3= 98√3
Example Question #1 : How To Simplify Square Roots
Simplify the following: (√(6) + √(3)) / √(3)
√(3)
None of the other answers
1
√(2) + 1
3√(2)
√(2) + 1
Begin by multiplying top and bottom by √(3):
(√(18) + √(9)) / 3
Note the following:
√(9) = 3
√(18) = √(9 * 2) = √(9) * √(2) = 3 * √(2)
Therefore, the numerator is: 3 * √(2) + 3. Factor out the common 3: 3 * (√(2) + 1)
Rewrite the whole fraction:
(3 * (√(2) + 1)) / 3
Simplfy by dividing cancelling the 3 common to numerator and denominator: √(2) + 1
Example Question #3 : How To Simplify Square Roots
what is
√0.0000490
7
0.007
49
0.07
0.00007
0.007
easiest way to simplify: turn into scientific notation
√0.0000490= √4.9 X 10-5
finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:
√4.9 X 10-5 = √49 X 10-6
√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007
Example Question #32 : Basic Squaring / Square Roots
Simplify:
In order to take the square root, divide 576 by 2.
All SAT Math Resources
