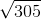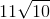All SAT Math Resources
Example Questions
Example Question #81 : Basic Squaring / Square Roots
Simplify:
To eliminate a radical expression, we need to multiply top and bottom by the conjugate which is opposite the sign in the expression. Then simplify if necessary.
Example Question #50 : How To Simplify Square Roots
Simplify:
To simplify square roots, we need to find perfect squares to factor out.

We can also simplify
Thus,
We can compute the numbers outside to get a final answer of 
Example Question #151 : Arithmetic
Simplify:
To eliminate a radical expression, we need to multiply top and bottom by the denominator.
Then simplify if necessary.
Example Question #1032 : Sat Mathematics
If 
In order to simplify the expression, we must see if we can factor out any perfect squares.
In this case, we can factor out 16x2.
Because of the rules of square roots, this can be rewritten as:
Because 


Thus, we can rewrite as
Example Question #84 : Basic Squaring / Square Roots
Simplify:
To simplify square roots, factor the inside completely to find perfect squares:
Then separate into several roots being multiplied:
Simplify:
Example Question #2 : How To Find The Common Factors Of Squares
If m and n are postive integers and 4m = 2n, what is the value of m/n?
2
4
1/2
8
16
1/2
- 22 = 4. Also, following the rules of exponents, 41 = 1.
- One can therefore say that m = 1 and n = 2.
- The question asks to solve for m/n. Since m = 1 and n = 2, m/n = 1/2.
Example Question #51 : Simplifying Square Roots
Simplify:
When simplifying the square root of a number that may not have a whole number root, it's helpful to approach the problem by finding common factors of the number inside the radicand. In this case, the number is 24,300.
What are the factors of 24,300?
24,300 can be factored into:
When there are factors that appear twice, they may be pulled out of the radicand. For instance, 100 is a multiple of 24,300. When 100 is further factored, it is 
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267786/gif.latex)
But 243 can also be factored:
Following the same principle as for the 100, the problem would become![9\cdot 10\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267789/gif.latex)
9 and 10 may be multiplied together, yielding the final simplified answer of
Example Question #1 : Arithmetic
To solve the equation 
When a factor appears twice, we can take it out of the square root.
Now the numbers can be added directly because the expressions under the square roots match.
Example Question #1 : Other Squaring / Square Roots
The square root of 5184 is:
72
74
73
70
71
72
The easiest way to narrow down a square root from a list is to look at the last number on the squared number – in this case 4 – and compare it to the last number of the answer.
70 * 70 will equal XXX0
71 * 71 will equal XXX1
72 * 72 will equal XXX4
73 * 73 will equal XXX9
74 * 74 will equal XXX(1)6
Therefore 72 is the answer. Check by multiplying it out.
Example Question #82 : Basic Squaring / Square Roots
If 
1
10
2
5
9
9
All SAT Math Resources







































![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267782/gif.latex)
![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267774/gif.latex)
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267778/gif.latex)
![900\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267780/gif.latex)
![90\sqrt[2]{270}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267776/gif.latex)
![9\sqrt[2]{300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267781/gif.latex)
![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267783/gif.latex)
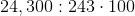


![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267790/gif.latex)