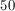We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Algebraic Fractions

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Algebraic Fractions

The maximum number of sweaters that Lauren can sew every day is equal to s, and the amount, in cents, that she charges for each sweater is equal to c. Which of the following expressions is equivalent to the maximum amount of money that Lauren can make, in dollars, after three weeks?

Possible Answers:

21sc/100

3c/(100s)

300c/s

2100s/c

2100sc

Correct answer:

21sc/100

Explanation:

The amount of money that Lauren can make depends on the number of sweaters that she can make. If she makes at most s sweaters a day, then we can multiply the number of days that she works by s to determine the total number of sweaters she makes.

total number of sweaters = (s)(number of days)

We are told to consider a time interval of three weeks. Because there are seven days in one week, the number of days over this period of time would equal 3(7), or 21 days. In other words, there are 21 days in three weeks Thus, the number of sweaters is equal to the product of s and 21.

total number of sweaters = (s)(21)

Now that we have the number of sweaters Lauren can make, we can multiply this by the cost of each sweater, which is equal to c cents, in order to obtain the amount of money she eared.

amount of money earned = (number of sweaters)(cost of each sweater)

amount of money earned = s(21)(c)

However, because the price of each sweater is given in terms of cents, the amount of money s(21)(c) will be equal to the number of cents she makes. The question, though, asks us to find the amount of money in dollars. We must use a conversion factor to change the number of cents to dollars. Remember that there are 100 cents per dollar.

Sweaters

Report an Error

Example Question #62 : Algebraic Fractions

If $\dpi{100} \small z>0$ , what is 40 percent of $\dpi{100} \small 30z$ ?

Possible Answers:

$\dpi{100} \small 12z$

$\dpi{100} \small 120z$

$\dpi{100} \small 5z$

$\dpi{100} \small 20z$

$\dpi{100} \small 30z$

Correct answer:

$\dpi{100} \small 12z$

Explanation:

To find 40 percent of $\dpi{100} \small 30z$ multiply $\dpi{100} \small 30z\times 0.4$

The result is $\dpi{100} \small 12z$

Report an Error

Example Question #6 : How To Solve For A Variable As Part Of A Fraction

Solve for .

$\frac{1}{3}(3x-6)+\frac{1}{2}(2x+4)=\frac{1}{5}(15x -5)$

Possible Answers:

$2$

$-2$

$0$

$-3$

Correct answer:

Explanation:

First distribute the fractions:

x-2 +x+2 =3x-1

Combine like terms:

2x=3x-1

x=1

Report an Error

Example Question #63 : Algebraic Fractions

Solve for $x$ .

$(2x+3)-3(x+5)=-(3x-4)$

Possible Answers:

$0$

$-8$

$-4$

$4$

Correct answer:

Explanation:

First distribute to eliminate the parentheses:

$2x+3-3x-15=-3x+4$

Then combine like terms:

$2x=16$

$x=8$

Report an Error

Example Question #64 : Algebraic Fractions

x = 1/2

What does 1/x + 1/(x + 4) equal?

Possible Answers:

4/9

9/2

20/9

Correct answer:

20/9

Explanation:

1/x + 1/(x+4) =

1/(1/2) + 1/ (1/2 + 4) =

1/ (1/2) + 1 / (9/2) =

2 + 2/9

20/9

Report an Error

Example Question #65 : Algebraic Fractions

Solve for .

$\frac{16}{x + 7} = \frac{2}{6}$

Possible Answers:

Correct answer:

Explanation:

Cross multiply. 96 = 2 (x+7)

Dsitribute. 96 = 2x + 14

Solve for . 96 - 14 = 2x

82 = 2x

41 = x

Report an Error

Example Question #1261 : Algebra

If x=-5 , what is the value of $\frac{x^{2}+20}{x-4}$ ?

Possible Answers:

Correct answer:

Explanation:

To solve this question, substitute -5 in for x in the numerator and denominator. Remember that the square of a negative number is positive.

45 / -9 = -5

Report an Error

Example Question #1156 : Algebra

Solve:

$\frac{4}{11}x + 3 = 15$

Possible Answers:

x = 39

x = 37

x = 29

$x = \frac{48}{11}$

x = 33

Correct answer:

x = 33

Explanation:

We want to isolate the x. First, we take away 3 from both sides. Then we have:

$\frac{4}{11}x = 12$

To get x by itself, we multiply by the reciprocal on both sides.

Then, we have:

$x = 12 \times \frac{11}{4} = \frac{12}{1}\times\frac{11}{4} = \frac{132}{4} = 33$

Report an Error

Example Question #66 : Algebraic Fractions

If $\frac{6}{x}=\frac{9}{19}$ , then what is the value of ?

Possible Answers:

9/114

7/12

38/3

3/38

none of these

Correct answer:

38/3

Explanation:

cross multiply:

(6)(19) = 9x

114=9x

x = 38/3

Report an Error

Example Question #67 : Algebraic Fractions

$\dpi{100} \small \frac{4 }{x} = \frac{2}{25}$

Find x.

Possible Answers:

$\dpi{100} \small \frac{25}{8}$

$\dpi{100} \small 0.25$

$\dpi{100} \small 50$

$\dpi{100} \small \frac{8}{25}$

None

Correct answer:

$\dpi{100} \small 50$

Explanation:

Cross multiply:

$\dpi{100} \small 4 \times 25 = 2x$

$\dpi{100} \small 100 = 2x$

$\dpi{100} \small x = 50$

Report an Error

View SAT Mathematics Tutors

Alexandra
Certified Tutor

Georgia State University, Bachelor of Fine Arts, Studio Art (Photography).

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in San Diego, Spanish Courses & Classes in Los Angeles, Spanish Courses & Classes in Atlanta, ISEE Courses & Classes in Houston, LSAT Courses & Classes in Miami, SSAT Courses & Classes in Chicago, ISEE Courses & Classes in Boston, ISEE Courses & Classes in Washington DC, ACT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Atlanta

Popular Test Prep

ACT Test Prep in Seattle, ISEE Test Prep in New York City, ISEE Test Prep in Houston, MCAT Test Prep in Houston, SAT Test Prep in Dallas Fort Worth, ISEE Test Prep in San Francisco-Bay Area, SAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Denver, LSAT Test Prep in Seattle, MCAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Algebraic Fractions

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #61 : Algebraic Fractions

Example Question #62 : Algebraic Fractions

Example Question #6 : How To Solve For A Variable As Part Of A Fraction

Example Question #63 : Algebraic Fractions

Example Question #64 : Algebraic Fractions

Example Question #65 : Algebraic Fractions

Example Question #1261 : Algebra

Example Question #1156 : Algebra

Example Question #66 : Algebraic Fractions

Example Question #67 : Algebraic Fractions

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: