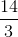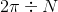We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : Graphing Functions

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 Next →

Example Question #1 : Graphing Trigonometric Functions

Which of these functions has a graph with amplitude $\frac{4}{7}$ ?

Possible Answers:

$f(x)=\sin \frac{4x}{7}$

$f(x)=\sin \frac{4 \pi x}{7}$

$f(x)= \frac{4}{7} \sin x$

$f(x)=\sin \frac{7x}{4}$

$f(x)= \frac{2}{7} \sin x$

Correct answer:

$f(x)= \frac{4}{7} \sin x$

Explanation:

The functions in each of the choices take the form of a sine function

$f(x)= A \sin Bx$ .

The graph of a sine function in this form has amplitude . Therefore, for this function to have amplitude 4, $A = \frac{4}{7}$ . Of the five choices, only

$f(x)= \frac{4}{7} \sin x$

matches this description.

Report an Error

Example Question #1 : Graphing Trigonometric Functions

Which of the following sine functions has a graph with period of 7?

Possible Answers:

$f(x)= \frac{11}{5} \sin \frac{7 x}{2}$

$f(x)= \frac{11}{5} \sin \frac{7 \pi x}{2}$

$f(x)= \frac{11}{5} \sin \frac{2 x}{7}$

$f(x)= \frac{11}{5} \sin \frac{2 \pi x}{7}$

$f(x)= \frac{11}{5} \sin \frac{ \pi x}{7}$

Correct answer:

$f(x)= \frac{11}{5} \sin \frac{2 \pi x}{7}$

Explanation:

The period of the graph of a sine function $f(x)= A \sin B x$ , is $\frac{2 \pi}{B}$ , or $2 \pi \div B$ .

Therefore, we solve for :

$\frac{2 \pi}{B} = 7$

$\frac{B}{2 \pi} = \frac{1}{7}$

$B= \frac{1}{7} \cdot 2 \pi = \frac{2 \pi}{7}$

The correct choice is therefore $f(x)= \frac{11}{5} \sin \frac{2 \pi x}{7}$ .

Report an Error

Example Question #1 : Find The Amplitude Of A Sine Or Cosine Function

Which of the given functions has the greatest amplitude?

Possible Answers:

$\sin(x+3)$

$2\sin(x)$

$\sin(4x)$

$\sin\frac{2\pi }{3}(x+2)$

$\frac{1}{2}\sin(4x)$

Correct answer:

$2\sin(x)$

Explanation:

The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is $2\sin(x)$ .

The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.

Report an Error

Example Question #1 : Graphing Piecewise And Recusive Functions

Define a function as follows:

$g(x) = \left\{\begin{matrix} x^{2}-6x-7 &x\le -5 \\ 6-x & -5 < x \le 0 \\ x+6 &0< x \le 5\\ x^{2}-x- 6& x> 5 \end{matrix}\right.$

How many -intercept(s) does the graph of have?

Possible Answers:

Four

None

Two

Three

One

Correct answer:

None

Explanation:

To find the -coordinates of possible -intercepts, set each of the expressions in the definition equal to 0, making sure that the solution is on the interval on which is so defined.

$g(x)= x^{2}-6x-7$ on the interval $(-\infty, -5]$

g(x) = 0

$x^{2}-6x-7 = 0$

(x+1)(x-7)= 0

x= -1 or x= 7

However, neither value is in the interval $(-\infty, -5]$ , so neither is an -intercept.

g(x)= 6-x on the interval ( -5, 0]

g(x) = 0

6-x = 0

$x = 6 \;$

However, this value is not in the interval ( -5, 0] , so this is not an -intercept.

g(x) =0 on the interval (0, 5]

x+ 6 = 0

x = -6

However, this value is not in the interval (0, 5] , so this is not an -intercept.

$g(x)= x^{2}-x- 6$ on the interval $(5, \infty)$

g(x)= 0

$x^{2}-x- 6 = 0$

(x+2) (x- 3)= 0

x= -2,x= 3

However, neither value is in the interval $(5, \infty)$ , so neither is an -intercept.

The graph of has no -intercepts.

Report an Error

Example Question #2 : Graphing Piecewise And Recusive Functions

Define a function as follows:

$g(x) = \left\{\begin{matrix} 6-x &x\le -5 \\ x^{2}-6x-7 & -5 < x \le 0 \\x^{2}-x- 6 &0< x \le 5\\x+6 & x> 5 \end{matrix}\right.$

How many -intercept(s) does the graph of have?

Possible Answers:

One

Two

Four

Three

None

Correct answer:

Two

Explanation:

To find the -coordinates of possible -intercepts, set each of the expressions in the definition equal to 0, making sure that the solution is on the interval on which is so defined.

g(x)= 6-x on the interval $(-\infty, -5]$

g(x) = 0

6-x = 0

$x = 6 \;$

However, this value is not in the interval ( -5, 0] , so this is not an -intercept.

$g(x)= x^{2}-6x-7$ on the interval ( -5, 0]

g(x) = 0

$x^{2}-6x-7 = 0$

(x+1)(x-7)= 0

x= -1 or x= 7

x= -1 is on the interval ( -5, 0] , so (-1,0) is an -intercept.

$g(x)= x^{2}-x- 6$ on the interval (0, 5]

g(x)= 0

$x^{2}-x- 6 = 0$

(x+2) (x- 3)= 0

x= -2,x= 3

x=3 is on the interval (0, 5] , so (3,0) is an -intercept.

g(x) =0 on the interval $(5, \infty)$

x+ 6 = 0

x = -6

However, this value is not in the interval $(5, \infty)$ , so this is not an -intercept.

The graph has two -intercepts, (-1,0) and (3,0) .

Report an Error

Example Question #1 : Graphing Piecewise And Recusive Functions

Define function as follows:

$g(x) = \left\{\begin{matrix} x^{2}-2x+7 &x\le -1 \\ 9-x & -1 < x \le 0 \\ x+8 &0< x \le 1 \\ x^{2}+3x+ 6& x> 1 \end{matrix}\right.$

Give the -intercept of the graph of the function.

Possible Answers:

(0, 8)

(0, 7)

(0, 6)

(0, 9)

The graph does not have a -intercept.

Correct answer:

(0, 9)

Explanation:

To find the -intercept, evaluate g(0) using the definition of on the interval that includes the value 0. Since

g(x)= 9-x

on the interval (-1, 0] ,

evaluate:

g(0)= 9-0 = 9

The -intercept is (0, 9) .

Report an Error

Example Question #1 : Graphing Piecewise And Recusive Functions

Define a function as follows:

$g(x) = \left\{\begin{matrix} \sin \frac{x}{2} -1 &x\le - \pi \\ \cos 2x & -\pi < x \le 0 \\ 1-\tan \frac{x }{2}&0< x < \pi \\ 0 & x\ge \pi \end{matrix}\right.$

At which of the following values of is discontinuous?

I) $x = -\pi$

II) x= 0

III) $x= \pi$

Possible Answers:

I and III only

I and II only

II and III only

All of I, II, and III

None of I, II, and III

Correct answer:

I and III only

Explanation:

To determine whether is continuous at $x = -\pi$ , we examine the definitions of on both sides of $-\pi$ , and evaluate both for $x = -\pi$ :

$\sin \frac{x}{2} -1$ evaluated for $x = -\pi$ :

$\sin \frac{-\pi}{2} -1 = \sin \left (- \frac{ \pi}{2} \right )-1= -1-1= -2$

$\cos 2x$ evaluated for $x = -\pi$ :

$\cos 2(-\pi) = \cos (-2\pi)= 1$

Since the values do not coincide, is discontinuous at $x = -\pi$ .

We do the same thing with the other two boundary values 0 and $\pi$ .

$\cos 2x$ evaluated for x =0 :

$\cos 2(0) = \cos 0= 1$

$1-\tan \frac{x }{2}$ evaluated for x =0 :

$1-\tan \frac{0 }{2} = 1 - \tan 0= 1-0 = 1$

Since the values coincide, is continuous at x =0 .

$1-\tan \frac{\pi }{2}$ turns out to be undefined for $x = \pi$ , (since $\tan \frac{\pi }{2}$ is undefined), so is discontinuous at $x = \pi$ .

The correct response is I and III only.

Report an Error

Example Question #5 : Graphing Piecewise And Recusive Functions

Define a function as follows:

$g(x) = \left\{\begin{matrix} x^{2}-2x+7 &x\le -1 \\ 9-x & -1 < x \le 0 \\ x+8 &0< x \le 1 \\ x^{2}+3x+ 6& x> 1 \end{matrix}\right.$

At which of the following values of is the graph of discontinuous?

I) x = -1

II) x= 0

III) x= 1

Possible Answers:

I and II only

II and III only

All of I, II, and III

None of I, II, and III

I and III only

Correct answer:

II and III only

Explanation:

To determine whether is continuous at x = -1 , we examine the definitions of on both sides of , and evaluate both for x = -1 :

$x^{2}-2x+7$ evaluated for x = -1 :

$(-1)^{2}-2(-1)+7= 1+2+7 = 10$

9-x evaluated for x = -1 :

9-(-1)= 10

Since the values coincide, the graph of is continuous at x = -1 .

We do the same thing with the other two boundary values 0 and 1:

9-x evaluated for x = 0 :

9-0= 9

x+8 evaluated for x = 0 :

0+8 = 8

Since the values do not coincide, the graph of is discontinuous at x = 0 .

x+8 evaluated for x = 1 :

1+8 = 9

$x^{2}+3x+ 6$ evaluate for x = 1 :

$1^{2}+3\cdot 1+ 6 = 1+ 3 + 6 = 10$

Since the values do not coincide, the graph of is discontinuous at x = 1 .

II and III only is the correct response.

Report an Error

Example Question #6 : Graphing Piecewise And Recusive Functions

Define a function as follows:

$g(x) = \left\{\begin{matrix} \sin \frac{x}{2} -1 &x\le - \pi \\ \cos 2x & -\pi < x \le 0 \\ 1-\tan \frac{x }{2}&0< x < \pi \\ 0 & x\ge \pi \end{matrix}\right.$

Give the -intercept of the graph of the function.

Possible Answers:

(0, -1)

The graph does not have a -intercept.

(0, -2)

(0, 1)

(0,0)

Correct answer:

(0, 1)

Explanation:

To find the -intercept, evaluate g(0) using the definition of on the interval that includes the value 0. Since

$g(x)= \cos 2x$

on the interval $(-\pi, 0]$ ,

evaluate:

$g(x)= \cos 2 \cdot 0 = \cos 0 = 1$

The -intercept is (0, 1) .

Report an Error

Example Question #91 : Functions And Graphs

Give the period of the graph of the equation

$f(x) = \frac{4}{7} \cos \left ( \frac{3\pi x}{7} \right )$

Possible Answers:

$\frac{4}{7}$

$\frac{2}{7}$

$\frac{7}{3}$

$\frac{14}{3}$

$\frac{8}{7}$

Correct answer:

$\frac{14}{3}$

Explanation:

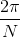
The period of the graph of a cosine function $f(x)= A \cos Nx$ is $\frac{2 \pi}{N}$ , or $2 \pi \div N$

Since $N = \frac{3\pi}{7}$ , the period is

$2 \pi \div \frac{3\pi}{7} = \frac{2 \pi }{1}\times \frac{7} {3\pi}= \frac{14}{3}$

Report an Error

← Previous 1 2 Next →

View SAT Subject Test in Mathematics Level 2 Tutors

Jaroslaw
Certified Tutor

Heriot Watt University, Master of Science, Physics. Heriot Watt University, Doctor of Science, Theoretical and Mathematical P...

View SAT Subject Test in Mathematics Level 2 Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View SAT Subject Test in Mathematics Level 2 Tutors

Luu Chi Hieu
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Los Angeles, ISEE Tutors in Seattle, SAT Tutors in Washington DC, GMAT Tutors in Miami, Calculus Tutors in Boston, SSAT Tutors in Phoenix, ISEE Tutors in Dallas Fort Worth, ACT Tutors in Seattle, English Tutors in Denver, Computer Science Tutors in Chicago

Popular Courses & Classes

LSAT Courses & Classes in Chicago, SAT Courses & Classes in New York City, GMAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Philadelphia, ISEE Courses & Classes in San Diego, ISEE Courses & Classes in Atlanta, SAT Courses & Classes in Seattle, GRE Courses & Classes in San Diego, LSAT Courses & Classes in San Diego, ISEE Courses & Classes in Seattle

Popular Test Prep

GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Boston, GRE Test Prep in Seattle, GMAT Test Prep in Washington DC, GRE Test Prep in Washington DC, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in Miami, SSAT Test Prep in San Diego, MCAT Test Prep in New York City, GRE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : Graphing Functions

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : Graphing Trigonometric Functions

Example Question #1 : Graphing Trigonometric Functions

Example Question #1 : Find The Amplitude Of A Sine Or Cosine Function

Example Question #1 : Graphing Piecewise And Recusive Functions

Example Question #2 : Graphing Piecewise And Recusive Functions

Example Question #1 : Graphing Piecewise And Recusive Functions

Example Question #1 : Graphing Piecewise And Recusive Functions

Example Question #5 : Graphing Piecewise And Recusive Functions

Example Question #6 : Graphing Piecewise And Recusive Functions

Example Question #91 : Functions And Graphs

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: