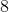Using the Product of Powers Rule, then the Power of a Power Rule, rewrite the first term:

Substitute  for ; the equation becomes

which is quadratic in terms of . The trinomial might be factorable using the  method, where we split the middle term with integers whose product is  and whose sum is . By trial and error, we find the integers to be  and , so the equation can be rewritten as follows:

Factoring by grouping:

By the Zero Product Rule, one of these two factors must be equal to 0.

If , then .

Since , then substituting this as well as substituting  back for , we get

, 

and

If , then

Since , then substituting this as well as substituting  back for , we get 

, and

The solution set is therefore 

Using the Product of Powers Rule, then the Power of a Power Rule, rewrite the first term:

Substitute  for ; the equation becomes

,

which is quadratic in terms of . The trinomial might be factorable using the  method, where we split the middle term with integers whose product is  and whose sum is 11. By trial and error, we find the integers to be 12 and , so the equation can be written as follows:

Factoring by grouping:

By the Zero Product Rule, one of these two factors must be equal to 0.

If , then .

Substituting  back for , we get

.

This is impossible, since any power of a positive number must be positive.

If , then:

Substituting  back for , we get

Since ,

it holds that , and , the only solution.

One of the properties of log is that 

Applying that principle to this problem:

Simplifying the log base 10

Plug in the values to the first equation:

An exponential base raised to the natural log will eliminate, leaving only the terms of the power.  This is a log rule that can be used to simplify the expression.

Distribute the x variable through the binomial.

The answer is:  

By the Power of a Power and Product of Power Rules, we can rewrite this equation as

Substitute  for ; the resulting equation is the quadratic equation

,

which can be written in standard form by subtracting  from both sides:

The quadratic trinomial fits the perfect square trinomial pattern:

By the square root principle,

Substituting  for :

Take the natural logarithm of both sides:

By Logarithm of a Power Rule, the above becomes

After distributing, solve for :

Factor out the left side, then divide:

Substituting the values of the logarithms:

This rounds to 0.45.

, so the equation 

can be rewritten as:

By the Power of a Power rule:

It follows that

Solving for :

Substitute  in the expression:

To simplify, we must first simplify the absolute values.

Now, combine like terms:

To solve for x we need to make two separate equations. Since it has absolute value bars around it we know that the inside can equal either 7 or -7 before the asolute value is applied.