All SAT II Math I Resources
Example Questions
Example Question #51 : Sat Subject Test In Math I
How many elements are in a set that has exactly 128 subsets?
None of the other responses is correct.
A set with elements has subsets.
Solve:
Example Question #1 : Mathematical Relationships
Rewrite as a single logarithmic expression:
Using the properties of logarithms
and ,
we simplify as follows:
Example Question #1 : Exponents And Logarithms
Solve:
In order to solve this problem, covert 27 to the correct base and power.
Since , the correct answer is .
Example Question #51 : Sat Subject Test In Math I
Simplify
When an exponent is raised by another exponent, we just multiply the powers.
Example Question #2 : Exponents And Logarithms
Simplify:
When adding exponents, we don't add the exponents or multiply out the bases. Our goal is to see if we can factor anything. We do see three . Let's factor.
Remember when multiplying exponents, we just add the powers.
Example Question #54 : Sat Subject Test In Math I
Solve and simplify.
Another way to write this is . The only number that makes is .
Example Question #55 : Sat Subject Test In Math I
Simplify:
is the same as . Let's factor out . It's the same as . Therefore which is the answer to our question.
Example Question #52 : Sat Subject Test In Math I
Simplify:
When dealing with subtraction in regards to logarithms, it's the same as dividing the numbers.
Example Question #53 : Sat Subject Test In Math I
Simplify:
When dealing with addition in regards to logarithms, it's the same as multiplying the numbers.
Example Question #58 : Sat Subject Test In Math I
Solve: when .
Power rule says when an exponent is raised to another exponent, you must multiply the exponents.
So and our expression is now .
Plug in the given value to get
.
Certified Tutor
All SAT II Math I Resources

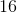

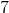











































![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/671897/gif.latex)



![5\sqrt[3]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/671871/gif.latex)

![\sqrt[3]{125}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/671898/gif.latex)









































