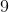Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #82 : Solid Geometry

Find the volume of a tetrahedron if the side length is $\frac{1}{6}$ .

Possible Answers:

$\frac{3\sqrt2}{2}$

$\frac{\sqrt2}{2592}$

$\frac{\sqrt2}{16}$

$\frac{\sqrt2}{216}$

$\frac{\sqrt2}{1296}$

Correct answer:

$\frac{\sqrt2}{2592}$

Explanation:

Write the equation to find the volume of a tetrahedron.

$V=\frac{a^3}{6\sqrt2}$

Substitute the side length and solve for the volume.

$V=\frac{(\frac{1}{6})^3}{6\sqrt2}= \frac{1}{216}\left(\frac{1}{6\sqrt2}\right)= \frac{1}{1296\sqrt2}$

Rationalize the denominator.

$V=\frac{1}{1296\sqrt2} \cdot \frac{\sqrt2}{\sqrt2}= \frac{\sqrt2}{1296\cdot 2} = \frac{\sqrt2}{2592}$

Report an Error

Example Question #82 : Solid Geometry

What is the volume of a regular tetrahedron with an edge length of 6?

Possible Answers:

25.5

32.1

26.6

24.2

27.8

Correct answer:

25.5

Explanation:

The volume of a tetrahedron can be solved for by using the equation:

$V= \frac{a^3}{6\sqrt{2}}$

where is the measurement of the edge of the tetrahedron.

This problem can be quickly solved by substituting 6 in for .

$V=\frac{6^3}{6\sqrt{2}}=\frac{216}{6\sqrt{2}}=\frac{36}{\sqrt{2}}$

${\color{Blue} V=25.5}$

Report an Error

Example Question #21 : Volume

What is the volume of the tetrahedron shown below?

Screen shot 2015 10 21 at 7.16.10 pm

Possible Answers:

$\frac{256}{6\sqrt2}$

$\frac{256}{3\sqrt2}$

$\frac{36}{\sqrt2}$

25.63

512

Correct answer:

$\frac{256}{3\sqrt2}$

Explanation:

The volume of a tetrahedron is $V=\frac{s^3}{6\sqrt2}$ .

This tetrahedron has a side with a length of 8.

$V=\frac{8^3}{6\sqrt2}$ , which becomes $\frac{512}{6\sqrt2}$ .

You can reduce that answer further, so that it becomes

$\frac{256}{3\sqrt2}$ .

Report an Error

Example Question #21 : Volume

Find the volume of sphere whose radius is 15.

Possible Answers:

$562.5\pi$

$4500\pi$

$36000\pi$

$1200\pi$

$300\pi$

Correct answer:

$4500\pi$

Explanation:

The volume of a sphere is given by the equation:

$V=\frac{4}{3} \pi r^3$

The problem says that the radius is 15, so plug in 15 for r and simplify.

$V=\frac{4}{3} \pi r^3=\frac{4}{3} \pi 15^3=4500\pi$

Report an Error

Example Question #22 : Volume

Find the volume of a sphere with the diameter of .

Possible Answers:

$12\pi$

$9\pi$

$27\pi$

$\frac{9}{4}\pi$

$\frac{9}{2}\pi$

Correct answer:

$\frac{9}{2}\pi$

Explanation:

Write the equation for the volume of a sphere.

$V=\frac{4}{3}\pi r^3$

The radius is half the diameter, or $\frac{3}{2}$ .

Substitute the radius into the equation.

$V=\frac{4}{3}\pi( \frac{3}{2})^3$

$V=\frac{4}{3}\pi( \frac{27}{8})$

Reduce the fractions.

The answer is: $\frac{9}{2}\pi$

Report an Error

Example Question #22 : 3 Dimensional Geometry

Determine the volume of a rectangular prism if the length is $\frac{1}{2}$ , width is $\frac{2}{3}$ , and the height is $\frac{5}{6}$ .

Possible Answers:

$\frac{1}{3}$

$\frac{2}{3}$

$\frac{9}{5}$

$\frac{5}{18}$

$\frac{5}{9}$

Correct answer:

$\frac{5}{18}$

Explanation:

Write the formula for the volume of a rectangular prism.

$A=\textup{ (Length) (Width) (Height)}$

Substitute the dimensions into the formula.

$A = \frac{1}{2}\cdot \frac{2}{3}\cdot \frac{5}{6} = \frac{10}{36}$

Reduce this fraction.

$\frac{5\times 2}{18\times 2}$

The answer is: $\frac{5}{18}$

Report an Error

Example Question #24 : Volume

The length of a box is half its height and two-thirds its width. The volume of the box is four cubic meters. Give the length of the box to the nearest centimeter.

Possible Answers:

$144 \textrm{ cm}$

None of these

$229\textrm{ cm}$

$175 \textrm{ cm}$

$110 \textrm{ cm}$

Correct answer:

$110 \textrm{ cm}$

Explanation:

Call , , and the length, width, and height of the crate.

The length of the crate is half its height, so

$L = \frac{1}{2} H$

$2 \cdot L = 2 \cdot \frac{1}{2} H$

2 L = H

The length of the crate is two-thirds its width, so

$L = \frac{2}{3} W$

$\frac{3} {2} \cdot L = \frac{3} {2} \cdot \frac{2}{3} W$

$\frac{3} {2} L = W$

The dimensions of the crate in terms of are , $\frac{3} {2} L$ , and . The volume is their product:

V= LWH

Substitute:

LWH = V

$L \cdot \frac{3} {2} L \cdot 2L = 4$

$3 L ^{3} = 4$

Solve for :

$3 L ^{3} = 4$

$\frac{3 L ^{3} }{3} = \frac{4 }{3}$

$L ^{3} = \frac{4 }{3}$

$L =\sqrt[3]{ \frac{4 }{3}}$

$L \approx 1.101$ meters.

Since one meter comprises 100 centimeters, multiply by 100 to convert to centimeters:

$1.101 \cdot 100 = 110.1$ ,

which rounds to 110 centimeters.

Report an Error

Example Question #21 : 3 Dimensional Geometry

A circular swimming pool has diameter 32 meters and depth meters throughout. Which of the following expressions gives the total area of the inside of the pool, in square meters?

Possible Answers:

None of the other responses is correct.

$256\pi + 16 \pi t$

$512\pi + 32 \pi t$

$256\pi + 32 \pi t$

$512\pi + 16 \pi t$

Correct answer:

$256\pi + 32 \pi t$

Explanation:

The bottom of the pool is a circle with diameter 32, and, subsequently, radius half this, or 16; its area is

$B = \pi r^{2} = \pi \times 16^{2} = 256 \pi$

The side of the pool is the lateral surface of a cylinder with radius 16 and height ; the area of this is

$LA = 2 \pi r h = 2 \pi \cdot 16 \cdot t = 32 \pi t$

The area of the inside of the pool is the sum of these two, or

$A = 256 \pi + 32 \pi t$

Report an Error

Example Question #1 : Surface Area

A circular swimming pool at an apartment complex has diameter 50 feet and depth six feet throughout.

The apartment manager needs to get the interior of the swimming pool painted. The paint she wants to use covers 350 square feet per gallon. How many one-gallon cans of paint will she need to purchase?

Possible Answers:

The correct answer is not given among the other responses.

Correct answer:

Explanation:

The pool can be seen as a cylinder with depth (or height) six feet and a base with diameter 50 feet - and radius half this, or 25 feet.

The bottom of the pool - the base of the cylinder - is a circle with radius 25 feet, so its area is

$B = \pi r ^{2} = 3.14 \cdot 25 \cdot 25 = 1,962.5$ square feet.

Its side - the lateral face of the cylinder - has area

$LA = 2 \pi r h = 2 \cdot 3.14 \cdot 25 \cdot 6 = 942$ square feet.

Their sum - the total area to be painted - is 1,962.5 + 942 = 2,904.5 square feet. Since one gallon of paint covers 350 square feet, divide:

$2,904.5 \div 350 \approx 8.3$

Eight cans of paint and part of a ninth will be required, so the correct response is nine.

Report an Error

Example Question #1 : Surface Area

Example cylinder

Figure not drawn to scale.

Find the surface area of the cylinder above.

Possible Answers:

87.25 in²

122.14 in²

94.25 in²

73.44 in²

56.55 in²

Correct answer:

94.25 in²

Explanation:

In order to find the surface area of a cylinder, you need to find the surface areas of the circles that are the top and bottom of the cylinder (2 x pi x radius²) and add it to the surface are of the rectangle that is the side of the cylinder (diameter x height).

$\small \small \small \small Surface Area=(2\pi r{^2})+(\pi2r\times h)$

$\small \small (2\pi\times 3{^2})+(6\pi\times 2)$

$\small \small (6.28\times 9)+(18.84\times 2)$

$\small 56.54 + 37.70=94.25$

The surface area of the cylinder is 94.25 in²

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Benjamin
Certified Tutor

Portland State University, Bachelor of Science, Computer Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Subject Test in Mathematics Level 1 Tutors

Robert
Certified Tutor

Daytona State College, Bachelor in Arts, Teaching English as a Second Language (ESL).

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Dallas Fort Worth, Reading Tutors in San Francisco-Bay Area, Biology Tutors in Atlanta, SSAT Tutors in Washington DC, ISEE Tutors in Chicago, Calculus Tutors in Atlanta, ISEE Tutors in Atlanta, LSAT Tutors in Houston, LSAT Tutors in Washington DC, MCAT Tutors in Chicago

Popular Courses & Classes

SAT Courses & Classes in Denver, Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Washington DC, SAT Courses & Classes in Chicago, LSAT Courses & Classes in Seattle, SSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Phoenix, Spanish Courses & Classes in Houston, SSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Phoenix

Popular Test Prep

GMAT Test Prep in Phoenix, GRE Test Prep in Chicago, LSAT Test Prep in Houston, GRE Test Prep in Houston, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Atlanta, LSAT Test Prep in Boston, SSAT Test Prep in Philadelphia, MCAT Test Prep in Boston, MCAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #82 : Solid Geometry

Example Question #82 : Solid Geometry

Example Question #21 : Volume

Example Question #21 : Volume

Example Question #22 : Volume

Example Question #22 : 3 Dimensional Geometry

Example Question #24 : Volume

Example Question #21 : 3 Dimensional Geometry

Example Question #1 : Surface Area

Example Question #1 : Surface Area

The surface area of the cylinder is 94.25 in²

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback:

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #82 : Solid Geometry

Example Question #82 : Solid Geometry

Example Question #21 : Volume

Example Question #21 : Volume

Example Question #22 : Volume

Example Question #22 : 3 Dimensional Geometry

Example Question #24 : Volume

Example Question #21 : 3 Dimensional Geometry

Example Question #1 : Surface Area

Example Question #1 : Surface Area

The surface area of the cylinder is 94.25 in2

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

The surface area of the cylinder is 94.25 in²