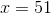Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #491 : Sat Subject Test In Math I

Regular Hexagon ABCDEF has perimeter 120. $\overline{AB }$ has as its midpoint; segment $\overline{MC}$ is drawn. To the nearest tenth, give the length of $\overline{MC}$ .

Possible Answers:

26.5

30.0

40.0

17.3

31.5

Correct answer:

26.5

Explanation:

The perimeter of the regular hexagon is 80, so each side measures one sixth of this, or 20. Also, since is the midpoint of $\overline{AB}$ , $AM = BM = \frac{1}{2}AB = \frac{1}{2} \cdot 20 = 10$ .

Also, each interior angle of a regular hexagon measures $120^{\circ }$ .

Below is the hexagon in question, with indicated and $\overline{MC}$ constructed; all relevant measures are marked.

Hexagon

A triangle $\bigtriangleup MBC$ is formed with MB = 10 , BC = 20 , and included angle measure $\angle B= 120 ^{\circ }$ . The length of the remaining side can be calculated using the Law of Cosines:

$c^{2} = a^{2} + b^{2} -2 ab \cos \gamma$

where and are the lengths of two sides, is the measure of their included angle, and is the length of the third side.

Setting $a = M B= 10, b= BC= 20 , \gamma= m \angle B = 120 ^{\circ }$ , and c = CM , substitute and evaluate :

$(CM)^{2} = 10^{2} + 20 ^{2} -2 (10) (20) \cos 120^{\circ }$

= 100 + 400 - 400 (-0.5)

= 500 + 200

$(CM)^{2} = 700$ ;

Taking the square root of both sides:

$CM \approx\sqrt{ 700} \approx 26.5$ ,

the correct choice.

Report an Error

Example Question #51 : Geometry

Regular Pentagon ABCDE has perimeter 80. $\overline{AB }$ has as its midpoint; segment $\overline{MC}$ is drawn. To the nearest tenth, give the length of $\overline{MC}$ .

Possible Answers:

20.9

25.9

20.0

18.8

15.5

Correct answer:

20.0

Explanation:

The perimeter of the regular pentagon is 80, so each side measures one fifth of this, or 16. Also, since is the midpoint of $\overline{AB}$ , $AM = BM = \frac{1}{2}AB = \frac{1}{2} \cdot 16 = 8$ .

Also, each interior angle of a regular pentagon measures $108^{\circ }$ .

Below is the pentagon in question, with indicated and $\overline{MC}$ constructed; all relevant measures are marked.

Pentagon 2

A triangle $\bigtriangleup MBC$ is formed with MB = 8 , BC = 16 , and included angle measure $\angle B= 108^{\circ }$ . The length of the remaining side can be calculated using the law of cosines:

$c^{2} = a^{2} + b^{2} -2 ab \cos \gamma$

where and are the lengths of two sides, $\gamma$ is the measure of their included angle, and is the length of the third side.

Setting $a = MB= 8, b= BC= 16, \gamma= m \angle B = 108^{\circ }$ , and c = CM , substitute and evaluate :

$(CM)^{2} = 8^{2} + 16^{2} -2 (8) (16) \cos 108^{\circ }$

$\approx 64 + 256 -256 (-0.3090)$

$\approx 320 +79.1$

$(CM)^{2} \approx 399.1$ ;

Taking the square root of both sides:

$CM \approx\sqrt{ 399.1} \approx 20.0$ ,

the correct choice.

Report an Error

Example Question #21 : Finding Sides

If the two legs of a right triangle are and , find the third side.

Possible Answers:

Correct answer:

Explanation:

Step 1: Recall the formula used to find the missing side(s) of a right triangle...

a^2+b^2=c^2

Step 2: Identify the legs and the hypotenuse in the formula...

a,b are the legs, and is the hypotenuse.

Step 3: Plug in the values of a and b given in the question...

a=5, b=12, c=?

(5)^2+(12)^2=c^2

$\Rightarrow 25+144=c^2$

$\Rightarrow 169=c^2$

$\Rightarrow c=\pm 13$

Step 3: A special rule about all triangles...

For any triangle, the measurements of any of the sides CANNOT BE zero.

So, the missing side is +13 , or

Report an Error

Example Question #493 : Sat Subject Test In Math I

Regular Pentagon ABCDE has perimeter 80. $\overline{AB }$ and $\overline{CD}$ have and as midpoints, respectively; segment $\overline{MN}$ is drawn. Give the length of $\overline{MN}$ to the nearest tenth.

Possible Answers:

25.9

18.8

20.0

15.5

20.9

Correct answer:

20.9

Explanation:

The perimeter of the regular pentagon is 80, so each side measures one fifth of this, or 16. Since is the midpoint of $\overline{AB}$ , $AM = BM = \frac{1}{2}AB = \frac{1}{2} \cdot 16 = 8$ .

Similarly, CN = DN= 8 .

Also, each interior angle of a regular pentagon measures $108^{\circ }$ .

Below is the pentagon with the midpoints and , and with $\overline{MN}$ constructed. Note that perpendiculars have been drawn to $\overline{MN}$ from and , with feet at points and , respectively.

Pentagon 2

BCYX is a rectangle, so XY = BC = 16 .

$\sin \angle MBX = \frac{MX}{MB}$ , or $MX = MB \cdot \sin \angle MBX$

$m \angle MBX = m \angle MBC- m \angle XBC = 108 ^{\circ } - 90 ^{\circ } = 18^{\circ }$ . Substituting:

$MX = 8 \cdot \sin 18^{\circ }$

$\approx 8 \cdot 0.3090$

$\approx 2.47$

For the same reason,

$NY \approx 2.47$ .

Adding the segment lengths:

$MN = MX + XY + NY \approx 2.47+ 16 + 2.47 \approx 20.94$ ,

Rond answer to the nearest tenth.

$MN \approx 20.9$

Report an Error

Example Question #61 : Geometry

Regular Pentagon ABCDE has a perimeter of eighty.

Give the length of diagonal $\overline{AC}$ to the nearest tenth.

Possible Answers:

18.8

20.9

25.9

15.5

20.0

Correct answer:

25.9

Explanation:

The perimeter of the regular pentagon is 80, so each side measures one fifth of this, or 16. Also, each interior angle of a regular pentagon measures $108^{\circ }$ .

The pentagon, along with diagonal $\overline{AC}$ , is shown below:

Pentagon 2

A triangle $\bigtriangleup ABC$ is formed with AB=BC = 16 , and included angle measure $\angle B= 108^{\circ }$ . The length of the remaining side can be calculated using the law of cosines:

$c^{2} = a^{2} + b^{2} -2 ab \cos \gamma$ ,

where and are the lengths of two sides, $\gamma$ the measure of their included angle, and the length of the side opposite that angle.

Setting $a = AB= 16, b= BC= 16, \gamma = m \angle B = 108^{\circ }$ , and c= AC , substitute and evaluate :

$(AC)^{2} = 16 ^{2} + 16^{2} -2 (16) (16) \cos 108^{\circ }$

$\approx 256 + 256 -512 (-0.3090)$

$\approx 512 + 158.21$

$(AC)^{2} \approx 670.21$

Taking the square root of both sides:

$AC \approx\sqrt{ 670.21 } \approx 25.9$ ,

the correct choice.

Report an Error

Example Question #141 : Quadrilaterals

ABCD is rhombus with side lengths in meters. $\overline{AB} = 13$ and $\overline{BD} = 10$ . What is the length, in meters, of $\overline{AC}$ ?

Rhombus_1

Possible Answers:

Correct answer:

Explanation:

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Rhombus_2

Thus, we can consider the right triangle AED to find the length of diagonal $\overline{AC}$ . From the given information, each of the sides of the rhombus measures meters and $\overline{BD} = 10$ .

Because the diagonals bisect each other, we know:

$\overline{AD} = 13$

$\overline{ED} = 5$

Using the Pythagorean theorem,

a^2 + b^2 = c^2

$\overline{AE}^2 + 5^2 = 13^2$

$\overline{AE}^2 = 144$

$\overline{AE} = 12$

$\overline{AC} = 24$

Report an Error

Example Question #1 : Finding Angles

What angle do the minute and hour hands of a clock form at 4:45?

Possible Answers:

$137 \frac{1}{2}^{\circ }$

$117 \frac{1}{2}^{\circ }$

$127 \frac{1}{2}^{\circ }$

$122\frac{1}{2}^{\circ }$

$132\frac{1}{2}^{\circ }$

Correct answer:

$127 \frac{1}{2}^{\circ }$

Explanation:

There are twelve numbers on a clock; from one to the next, a hand rotates $\left (\frac{360}{12} \right )^{\circ } = 30^{\circ }$ . At 4:45, the minute hand is exactly on the "9" - that is, at the $\left (30 \times 9 \right )^{\circ }= 270^{\circ }$ . The hour hand is three-fourths of the way from the "4" to the "5" - that is, on the $\left (4 \frac{3}{4} \times 30 \right )^{\circ } = 142 \frac{1}{2} ^{\circ }$ position. Therefore, the difference is the angle they make:

$\left (270 - 142 \frac{1}{2} \right ) ^{\circ } = 127 \frac{1}{2}^{\circ }$

Report an Error

Example Question #2 : Finding Angles

What angle do the minute and hour hands of a clock form at 8:50?

Possible Answers:

$55^{\circ }$

$35^ {\circ }$

$60^{\circ }$

$30^{\circ }$

$45^{\circ }$

Correct answer:

$35^ {\circ }$

Explanation:

There are twelve numbers on a clock; from one to the next, a hand rotates $\left (\frac{360}{12} \right )^{\circ } = 30^{\circ }$ . At 8:50, the minute hand is exactly on the "10" - that is, on the $\left (30 \times 10 \right )^{\circ }= 300^{\circ }$ position. The hour hand is five-sixth of the way from the "8" to the "9" - that is, on the $\left (8 \frac{5}{6} \times 30 \right )^{\circ } = 265 ^{\circ }$ position. Therefore, the difference is the angle they make:

$300^{\circ } - 265^{\circ } = 35^{\circ }$ .

Report an Error

Example Question #491 : Sat Subject Test In Math I

Hexagon

Note: Figure NOT drawn to scale.

The above hexagon is regular. What is ?

Possible Answers:

x = 66

x = 84

x =72

x = 51

x = 78

Correct answer:

x = 66

Explanation:

Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

$\frac{180^{\circ } (6-2)}{6}= 120^{\circ }$ .

The four angles of the quadrilateral are $120 ^{\circ }, 120^{\circ } , x^{\circ }, (x - 12)^{\circ }$ . Their sum is $360^{\circ }$ , so we can set up, and solve for in, the equation:

x +(x-12)+ 120 + 120 =360

2x-12+ 120 + 120 =360

2x+228 =360

2x =132

x = 66

Report an Error

Example Question #1 : Finding Angles

Can a triangle have a set of angles that are 90, 46, and degrees?

Possible Answers:

Yes

Correct answer:

Explanation:

A triangle's angles must add up to 180 degrees.

The angles given add up to 181,

(90+46+45=181) .

That means that this cannot be an actual triangle.

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Samarth
Certified Tutor

Maharaja Sayajirao University of Baroda, Bachelor of Engineering, Mechanical Engineering. Concordia University-Seward, Master...

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Boston, Spanish Tutors in Philadelphia, GRE Tutors in Dallas Fort Worth, ISEE Tutors in Miami, Biology Tutors in Dallas Fort Worth, English Tutors in New York City, Biology Tutors in Phoenix, Algebra Tutors in Dallas Fort Worth, GRE Tutors in Washington DC, Reading Tutors in Boston

Popular Courses & Classes

LSAT Courses & Classes in Houston, ISEE Courses & Classes in Los Angeles, ISEE Courses & Classes in San Diego, GMAT Courses & Classes in Chicago, SAT Courses & Classes in San Diego, SSAT Courses & Classes in Boston, GMAT Courses & Classes in Washington DC, GRE Courses & Classes in Miami, MCAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Boston

Popular Test Prep

SAT Test Prep in Boston, MCAT Test Prep in Boston, SSAT Test Prep in San Diego, MCAT Test Prep in Houston, SSAT Test Prep in Boston, ACT Test Prep in Washington DC, GMAT Test Prep in Washington DC, GMAT Test Prep in Chicago, SSAT Test Prep in Houston, SAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #491 : Sat Subject Test In Math I

Example Question #51 : Geometry

Example Question #21 : Finding Sides

Example Question #493 : Sat Subject Test In Math I

Example Question #61 : Geometry

Example Question #141 : Quadrilaterals

Example Question #1 : Finding Angles

Example Question #2 : Finding Angles

Example Question #491 : Sat Subject Test In Math I

Example Question #1 : Finding Angles

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: