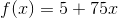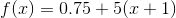All SAT II Math I Resources
Example Questions
Example Question #2 : Graphing Polynomial Functions
Which of the graphs best represents the following function?

None of these




The highest exponent of the variable term is two (
The graph below will be the answer, as it shows a parabolic curve.

Example Question #1 : Graphing Polynomial Functions
Which of the following is a graph for the following equation:
Cannot be determined

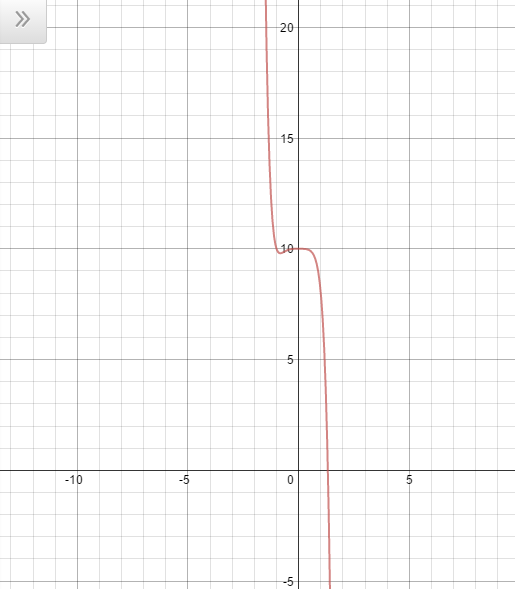



The way to figure out this problem is by understanding behavior of polynomials.
The sign that occurs before the 

Example Question #22 : Graphing Functions
Define a function 



Which of the following statements is correct about 
Define 


By the Intermediate Value Theorem (IVT), if 





Evaluate 
Only in the case of 





Example Question #1 : Solving Functions From Word Problems
At Joe's pizzeria a pizza costs $5 with the first topping, and then an additional 75 cents for each additional topping.
If 
Notice that the question describes a linear equation because there is a constant rate of change (the cost per topping). This means we can use slope intercept form to describe the scenario.
Recall that slope intercept form is
The value of 






Notice that the first topping is included in the $5 cost. The 
Putting all these steps together we get:
Example Question #1 : 2 Dimensional Geometry

The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely. However, because of the cutting device the pool store uses, the length and the width of the tarp must each be a multiple of three yards. Also, the tarp must be at least one yard longer and one yard wider than the pool.
What will be the minimum area of the tarp the manager purchases?
Three feet make a yard, so the length and width of the pool are 



The tarp must be 18 yards by 15 yards, so the area of the tarp is the product of these dimensions, or

Example Question #1 : 2 Dimensional Geometry

Note: Figure NOT drawn to scale.
Refer to the figure above, which shows a square inscribed inside a large triangle. What percent of the entire triangle has been shaded blue?
Insufficient information is given to answer the question.
The shaded portion of the entire triangle is similar to the entire large triangle by the Angle-Angle postulate, so sides are in proportion. The short leg of the blue triangle has length 20; that of the large triangle, 30. Therefore, the similarity ratio is 


The blue triangle is therefore 

Example Question #1 : Area

Note: Figure NOT drawn to scale.
Refer to the above diagram. What is the area of 
Insufficient information is given to answer the problem.
If we see hypotenuse 




The area of 
Example Question #1 : Area

The above figure depicts the rectangular swimming pool at an apartment. The apartment manager needs to purchase a tarp that will cover this pool completely, but the store will only sell the material in multiples of ten square yards. How many square yards will the manager need to buy?
Three feet make a yard, so the length and width of the pool are 


The manager will need to buy a number of square yards of tarp equal to the next highest multiple of ten, which is 200 square yards.
Example Question #1 : 2 Dimensional Geometry

Note: Figure NOT drawn to scale.
Refer to the above diagram. In terms of area, 

Insufficient information is given to answer this question.
The area of 
The area of 


Therefore, in terms of area, 


Example Question #1 : 2 Dimensional Geometry

Note: Figure NOT drawn to scale.
Refer to the above diagram. Give the ratio of the area of 

Insufficient information is given to answer the question.


The areas of 

The area of 
The area of 
The ratio of the areas is 
All SAT II Math I Resources