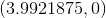SAT II Math I : Solving Functions
Study concepts, example questions & explanations for SAT II Math I
All SAT II Math I Resources
Example Questions
Example Question #9 : Solving Exponential Equations
Solve for 
Let's convert 
We know the following:
Simplify.
Solve.
Example Question #10 : Solving Exponential Equations
Solve for 
Let's convert 
We know the following:
Simplify.
Solve.
Example Question #11 : Solving Exponential Equations
Solve for 
When multiplying exponents with the same base, we will apply the power rule of exponents:
We will simply add the exponents and keep the base the same.
Example Question #11 : Solving Exponential Equations
Solve for 
When multiplying exponents with the same base, we will apply the power rule of exponents:
We will simply add the exponents and keep the base the same.
Simplify.
Solve.
Example Question #13 : Solving Exponential Equations
Solve for 
When adding exponents with the same base, we need to see if we can factor out the numbers of the base.
In this case, let's factor out 
We get the following:
Since we are now multiplying with the same base, we get the following expression:
Now we have the same base and we just focus on the exponents.
The equation is now:
Solve.
Example Question #14 : Solving Exponential Equations
Solve for 
First, we need to convert 
We know 
Therefore we can write the following expression:
Next, when we add exponents of the same base, we need to see if we can factor out terms.
In this case, let's factor out 
We get the following:
Since we are now multiplying with the same base, we get the following expression:
Now we have the same base and we just focus on the exponents.
The equation is now:
Solve.
Example Question #1 : Graphing Exponential Functions
Give the 
The graph has no 
The graph has no
Set 
We need not work further. It is impossible to raise a positive number 2 to any real power to obtain a negative number. Therefore, the equation has no solution, and the graph of 
Example Question #2 : Graphing Exponential Functions
What is/are the asymptote(s) of the graph of the function 
An exponential function of the form
has as its one and only asymptote the horizontal line 
Since we define 
then 
and the only asymptote is the line of the equation 
Example Question #3 : Graphing Exponential Functions
Determine whether each function represents exponential decay or growth.
a) growth
b) growth
a) decay
b) decay
a) decay
b) growth
a) growth
b) decay
a) decay
b) growth
a)
This is exponential decay since the base, 
b)
This is exponential growth since the base, 
Example Question #4 : Graphing Exponential Functions
Match each function with its graph.
1.
2.
3.
a.
b.
c.
1.
2.
3.
1.
2.
3.
1.
2.
3.
1.
2.
3.
1.
2.
3.
For 
For 
For 
All SAT II Math I Resources
