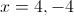We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Solving Functions

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 Next →

Example Question #3 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Find the vertical asymptote of the equation.

$y=\frac{x^2-9}{x^2-16}$

Possible Answers:

x=4, -4

x=1

x=0

x=4

There are no vertical asymptotes.

Correct answer:

x=4, -4

Explanation:

To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.

0=x^2-16

16=x^2

$\sqrt{16}=\sqrt{x^2}$

4, -4=x

Report an Error

Example Question #3 : Solving And Graphing Exponential Equations

Consider the exponential function y=2^x+3 . Determine if there are any asymptotes and where they lie on the graph.

Possible Answers:

There are no asymptotes. goes to positive infinity in both the and directions.

There is one horizontal asymptote at y=3 .

There is one vertical asymptote at y=2 .

There is one vertical asymptote at y=3 .

Correct answer:

There is one horizontal asymptote at y=3 .

Explanation:

For positive values, increases exponentially in the direction and goes to positive infinity, so there is no asymptote on the positive -axis. For negative values, as decreases, the term 2^x becomes closer and closer to zero so approaches as we move along the negative axis. As the graph below shows, this is forms a horizontal asymptote.

Exp_asymp

Report an Error

Example Question #1 : Solving And Graphing Exponential Equations

Solve the equation for .

$\small 9^x=3^6$

Possible Answers:

$\small x=3$

$\small x=0$

$\small x=1$

$\small x=2$

Correct answer:

$\small x=3$

Explanation:

Begin by recognizing that both sides of the equation have a root term of .

$\small 9^x=3^6$

(3^2)^x=3^6

Using the power rule, we can set the exponents equal to each other.

$3^{(2*x)}=3^6$

$\small 2x=6$

$\small x=3$

Report an Error

Example Question #2 : Solving And Graphing Exponential Equations

Solve the equation for .

$\small 3^{2x}=81$

Possible Answers:

x=2

x=1

x=4

x=9

x=3

Correct answer:

x=2

Explanation:

Begin by recognizing that both sides of the equation have the same root term, .

$\small 3^{2x}=81$

$\small 3^{2x}=9^2$

$3^{2x}=(3^2)^2$

We can use the power rule to combine exponents.

$3^{2x}=3^4$

Set the exponents equal to each other.

2x=4

$\small x=2$

Report an Error

Example Question #3781 : Algebra Ii

In 2009, the population of fish in a pond was 1,034. In 2013, it was 1,711.

Write an exponential growth function of the form $y=ab^{x}}$ that could be used to model , the population of fish, in terms of , the number of years since 2009.

Possible Answers:

y=1.35(1.0011)^x

y=1711(1.3932)^x

y=1.2(1711)^x

y=1.1(1034)^x

y=1034(1.1342)^x

Correct answer:

y=1034(1.1342)^x

Explanation:

Solve for the values of a and b:

In 2009, y=1034 and x=0 (zero years since 2009). Plug this into the exponential equation form:

$1034=ab^{(0)}$ . Solve for to get .

In 2013, y=1711 and x=4 . Therefore,

1711=ab^4 or 1711=(1034)b^4 . Solve for to get

$b=\sqrt[4]{\frac{1711}{1034}}\approx1.1342$ .

Then the exponential growth function is

$y=1034(1.1342)^{x}$ .

Report an Error

Example Question #4 : Solving Exponential Equations

$4^{5x}=8^{4x-1}$

Solve for .

Possible Answers:

1.5

Correct answer:

1.5

Explanation:

8 and 4 are both powers of 2.

$4^{5x}=8^{4x-1}$

$2^{10x}=2^{12x-3}$

10x=12x-3 -2x=-3 x=1.5

Report an Error

Example Question #5 : Solving Exponential Equations

Solve for :

$80^{2x+3}=80^{5x-9}$

Possible Answers:

x=4

$x=\frac{1}{4}$

x=80

No solution

x=2

Correct answer:

x=4

Explanation:

Because both sides of the equation have the same base, set the terms equal to each other.

2x+3=5x-9

Add 9 to both sides: 2x+12=5x

Then, subtract 2x from both sides: 12=3x

Finally, divide both sides by 3: x=4

Report an Error

Example Question #1 : Solving Exponential Equations

Solve for :

$25^{-x+5}=125^{6x-10}$

Possible Answers:

x=2

x=5

$x=\frac{1}{2}$

$x=\frac{15}{7}$

No solution

Correct answer:

x=2

Explanation:

125 and 25 are both powers of 5.

Therefore, the equation can be rewritten as

$(5^3)^{6x-10}=(5^2)^{-x+5}$ .

Using the Distributive Property,

$5^{18x-30}=5^{-2x+10}$ .

Since both sides now have the same base, set the two exponents equal to one another and solve:

18x-30=-2x+10

Add 30 to both sides: 18x=-2x+40

Add to both sides: 20x=40

Divide both sides by 20: x=2

Report an Error

Example Question #7 : Solving Exponential Equations

Solve $9^{4x+2}=27^{3x-4}$ .

Possible Answers:

$x=\frac{-16}{9}$

x=6

x=3

x=16

No solution

Correct answer:

x=16

Explanation:

Both 27 and 9 are powers of 3, therefore the equation can be rewritten as

$(3^2)^{4x+2}=(3^3)^{3x-4}$ .

Using the Distributive Property,

$3^{8x+4}=3^{9x-12}$ .

Now that both sides have the same base, set the two exponenents equal and solve.

8x+4=9x-12

Add 12 to both sides: 8x+16=9x

Subtract from both sides: 16=x

Report an Error

Example Question #61 : Functions And Graphs

$(3)2^{x}=24$

Possible Answers:

x=3

x=4

x=-2

x=0

x=1

Correct answer:

x=3

Explanation:

The first step in thist problem is divide both sides by three: $2^{x}=8$ . Then, recognize that 8 could be rewritten with a base of 2 as well ( 2^3 ). Therefore, your answer is 3.

Report an Error

← Previous 1 2 3 4 5 6 7 8 Next →

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View SAT Subject Test in Mathematics Level 1 Tutors

Yi
Certified Tutor

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Philadelphia, GMAT Tutors in Miami, SSAT Tutors in San Francisco-Bay Area, Math Tutors in Phoenix, Statistics Tutors in Philadelphia, SAT Tutors in San Diego, Algebra Tutors in Dallas Fort Worth, Math Tutors in Miami, Physics Tutors in Atlanta, Chemistry Tutors in Seattle

Popular Courses & Classes

SSAT Courses & Classes in Miami, GMAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Houston, GRE Courses & Classes in Seattle, SAT Courses & Classes in Miami, GRE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Phoenix, Spanish Courses & Classes in New York City, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Philadelphia

Popular Test Prep

MCAT Test Prep in Dallas Fort Worth, SSAT Test Prep in San Diego, GRE Test Prep in Philadelphia, LSAT Test Prep in San Francisco-Bay Area, ACT Test Prep in New York City, MCAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Denver, LSAT Test Prep in Philadelphia, ACT Test Prep in Seattle, SAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Solving Functions

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #3 : Find The Equations Of Vertical Asymptotes Of Tangent, Cosecant, Secant, And Cotangent Functions

Example Question #3 : Solving And Graphing Exponential Equations

Example Question #1 : Solving And Graphing Exponential Equations

Example Question #2 : Solving And Graphing Exponential Equations

Example Question #3781 : Algebra Ii

Example Question #4 : Solving Exponential Equations

Example Question #5 : Solving Exponential Equations

Example Question #1 : Solving Exponential Equations

Example Question #7 : Solving Exponential Equations

Example Question #61 : Functions And Graphs

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: