All SAT II Math I Resources
Example Questions
Example Question #61 : Solving Functions
Find the roots of the following quadratic expression:
First, we have to know that "finding the roots" means "finding the values of x which make the expression =0." So basically we are going to set the original expression = 0 and factor.
This quadratic looks messy to factor by sight, so we'll use factoring by composition. We multiply a and c together, and look for factors that add to b.
So we can use 8 and -3. We will re-write 5x using these numbers as 8x - 3x, and then factor by grouping.
Note the extra + sign we inserted to make sure the meaning is not lost when parentheses are added. Now we identify common factors to be "pulled" out.
Now we factor out the (3x + 4).
Setting each factor = 0 we can find the solutions.
So the solutions are x = 1/2 and x = -4/3, or {-4/3, 1/2}.
Example Question #101 : Functions And Graphs
Find the roots of the following quadratic expression.
First we remember that "find the roots" means "find the values of x for which this expression equals 0." So we set the expression = 0 and approach solving as normal.
Since solving this by sight is difficult, we'll use composition, multiplying a by c and finding factors which add to b.
So -9 and 5 will work; we will use them to rewrite -4x as -9x + 5x and then factor by grouping.
We identify common factors to "pull" out of each group.
And now we factor out x-3.
Setting each factor equal to 0 lets us solve for x.
So our solutions are x = -5/3 and x = 3, which we write as x = {-5/3, 3}.
Example Question #102 : Functions And Graphs
FInd the roots for
Notice in this question there are only two terms, the exponent value and the constant value. There is also the negative sign between the two. When we look at each number we see that each are a perfect square. Due to the negative sign between the two, this type of quadratic expression can also be written as a difference of squares. We look at the exponential term and see it is
The perfect square factors of this term are 

Now we look at the constant term
The perfect square factors of this term are 
Now to combine these into the binomial factor form we need to remember it is the difference of perfect squares meaning we will have one subtraction sign and one adding sign, so we get the following:
From here we solve each binomial for x. To do this we set each binomal to zero and solve for x.




Example Question #103 : Functions And Graphs
Find the roots for
Notice in this question there are only two terms, the exponent value and the constant value. There is also the negative sign between the two. When we look at each number we see that each are a perfect square. Due to the negative sign between the two, this type of quadratic expression can also be written as a difference of squares. We look at the exponential term and see it is
The perfect square factors of this term are 

Now we look at the constant term
The perfect square factors of this term are 
Now to combine these into the binomial factor form we need to remember it is the difference of perfect squares meaning we will have one subtraction sign and one adding sign, so we get the following:
From here we solve each binomial for x. To do this we set each binomal to zero and solve for x.





Example Question #104 : Functions And Graphs
Find the roots for
Notice in this question there are only two terms, the exponent value and the constant value. There is also the negative sign between the two. When we look at each number we see that each are a perfect square. Due to the negative sign between the two, this type of quadratic expression can also be written as a difference of squares. We look at the exponential term and see it is
The perfect square factors of this term are 

Now we look at the constant term
The perfect square factors of this term are 

Now to combine these into the binomial factor form we need to remember it is the difference of perfect squares meaning we will have one subtraction sign and one adding sign, so we get the following:
From here we solve each binomial for x. To do this we set each binomal to zero and solve for x.



Example Question #105 : Functions And Graphs
Find the roots of 
Notice in this question there are only two terms, the exponent value and the constant value. There is also the negative sign between the two. When we look at each term we see that each is a perfect square. Due to the negative sign between the two, this type of quadratic expression can also be written as a difference of squares. We look at the exponential term and see it is
The perfect square factors of this term are 

Now we look at the constant term
The perfecct square factors of this term are 

Now to combine these into the binomial factor form we need to remember it is the difference of perfect squares meaning we will have one subtraction sign and one adding sign, so we get the following:
From here we solve each binomial for x. To do this we set each binomal to zero and solve for x.




Example Question #48 : Finding Roots
Find the roots,


This problem could be worked out using the quadratic formula, but in this particular case it's easier to factor the left side.


A few more points...
Observe that the coefficient for the 




If you notice this pattern in a quadratic, then factoring is always a faster approach. The quadratic formula will always work too, but may take a little longer.
Unfortunately you will often find that factoring is not an option since you will not always be abe to easily find such a pattern for most quadratics, especially if the roots are not whole number integers, or if one or both of the roots are complex numbers.
Example Question #1 : Completing The Square
Solve the following equation by completing the square. Use a calculator to determine the answer to the closest hundredth.
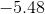


No solution

No solution
To solve by completing the square, you should first take the numerical coefficient to the “right side” of the equation:
Then, divide the middle coefficient by 2:
Square that and add it to both sides:
Now, you can easily factor the quadratic:
Your next step would be to take the square root of both sides. At this point, however, you know that you cannot solve the problem. When you take the square root of both sides, you will be forced to take the square root of 
Example Question #111 : Functions And Graphs
The product of two consective positive odd integers is 143. Find both integers.
If 

Distribute into the parenthesis.
Subtract 143 from both sides.
This can be solved by factoring, or by the quadratic equation. We will use the latter.
We are told that both integers are positive, so 
The other integer is 
Example Question #2 : Quadratic Inequalities
Solve:
Start by changing the less than sign to an equal sign and solve for 
Now, plot these two numbers on a number line.

Notice how the number line is divided into three regions:
Now, choose a number fromeach of these regions to plug back into the inequality to test if the inequality holds.
For 
Since this number is not less than zero, the solution cannot be found in this region.
For 
Since this number is less than zero, the solution can be found in this region.
For 

Since this number is not less than zero, the solution cannot be found in this region.
Because the solution is only negative in the interval 
All SAT II Math I Resources














































































































































