The dirt path can be seen as the region between two rectangles. The outer rectangle has length and width 100 feet and 60 feet, respectively, so its area is 

 square feet.

The inner rectangle has length and width  feet and  feet, respectively, so its area is

 square feet.

The area of the path is the difference of the two:

 square feet.

The area of the dirt path is the difference between the areas of the outer and inner rectangles.

The outer rectangle has area

The area of the inner rectangle can be found as follows:

The length of the garden is  feet less than that of the entire lot, or 

;

The width of the garden is  less than that of the entire lot, or 

;

The area of the garden is their product:

Now, subtract the areas:

The area of a square =

The area of a circle is

Area  = Area of Square  2(Area of Circle) =

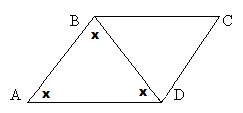
If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.

We now have two equilateral triangles, so all sides of the triangles will be equal.

All sides therefore equal 5.

5+5+5+5 = 20

You need to find two numbers that multiply to give 72 and add up to give 18

easiest way: write the multiples of 72:

1, 72

2, 36

3, 24

4, 18

6, 12: these add up to 18

 (x + 6)(x + 12)

Nothing common cancels at the beginning. To factor this, we need to find two numbers that multiply to 9 * 4 = 36 and sum to 12. 6 and 6 work.

So 9x² + 12x + 4 = 9x² + 6x + 6x + 4

Let's look at the first two terms and last two terms separately to begin with. 9x² + 6x can be simplified to 3x(3x + 2) and 6x + 4 can be simplified into 2(3x + 2). Putting these together gets us 

9x² + 12x + 4

= 9x² + 6x + 6x + 4

= 3x(3x + 2) + 2(3x + 2) 

= (3x + 2)(3x + 2)

This is as far as we can factor. 

The numerator on the left can be factored so the expression becomes , which can be simplified to

Then you can solve for  by adding 3 to both sides of the equation, so 

First, factor.

Set each factor equal to 0

Therefore,

Let's try to factor x² – y² – z² + 2yz.

Notice that the last three terms are very close to y² + z² – 2yz, which, if we rearranged them, would become y² – 2yz+ z². We could factor y² – 2yz+ z² as (y – z)², using the general rule that p² – 2pq + q² = (p – q)² .

So we want to rearrange the last three terms. Let's group them together first.

x² + (–y² – z² + 2yz)

If we were to factor out a –1 from the last three terms, we would have the following:

x² – (y² + z² – 2yz)

Now we can replace y² + z² – 2yz with (y – z)².

x² – (y – z)²

This expression is actually a differences of squares. In general, we can factor p² – q² as (p – q)(p + q). In this case, we can substitute x for p and (y – z) for q.

x² – (y – z)² = (x – (y – z))(x  + (y – z))

Now, let's distribute the negative one in the trinomial x – (y – z)

(x – (y – z))(x  + (y – z)) 

(x – y + z)(x + y – z)

The problem said that factoring x² – y² – z² + 2yz would result in two polynomials in the form (ax + by + cz)(dx + ey + fz), where a, b, c, d, e, and f were all integers, and a > 0.

(x – y + z)(x + y – z) fits this form. This means that a = 1, b = –1, c = 1, d = 1, e = 1, and f = –1. The sum of all of these is 2.

The answer is 2.