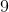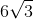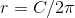First note that a clock is a circle made of 360 degrees, and that each number represents an angle and the separation between them is 360/12 = 30. And at 2:00, the minute hand is on the 12 and the hour hand is on the 2.  The correct answer is 2 * 30 = 60 degrees.

At four o’clock the minute hand is on the 12 and the hour hand is on the 4.  The angle formed is 4/12 of the total number of degrees in a circle, 360.

4/12 * 360 = 120 degrees

A clock is a circle, and a circle always contains 360 degrees. Since there are 60 minutes on a clock, each minute mark is 6 degrees.

The minute hand on the clock will point at 15 minutes, allowing us to calculate it's position on the circle.

Since there are 12 hours on the clock, each hour mark is 30 degrees.

We can calculate where the hour hand will be at 8:00.

However, the hour hand will actually be between the 8 and the 9, since we are looking at 8:15 rather than an absolute hour mark. 15 minutes is equal to one-fourth of an hour. Use the same equation to find the additional position of the hour hand.

We are looking for the angle between the two hands of the clock. The will be equal to the difference between the two angle measures.

A analog clock is divided up into 12 sectors, based on the numbers 1–12. One sector represents 30 degrees (360/12 = 30). If the hour hand is directly on the 10, and the minute hand is on the 2, that means there are 4 sectors of 30 degrees between then, thus they are 120 degrees apart (30 * 4 = 120).

First, we must determine where the hands are located at this time. The minute hand will be exactly on the three. The hour hand will be a little bit (15 mins) passed the seven. A circle has  in it, so because there are  numbers on a clock's face, each number is separated by

The angle between the  and the  is equal to  

Finally, we must figure out exactly how far past the  our hour hand is. If the hour hand moves  in , that means that it must move a half of a degree every minute. If we are  past , we can do 

Therefore, our hour hand has moved an extra  due to the  that have elapsed.

Our angle is equal to 

.

The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°.  One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.

To solve a chord problem, draw right triangles using the chord, the radii, and a line connecting the center of the circle to the chord at a right angle. 

Now, the chord is split into two equal pieces, and angle AOB is bisected. Instead of one 120 degree angle, you now have two 30-60-90 triangles. 30-60-90 triangles are characterized by having sides in the following ratio:

So, to find the length of the chord, first find the length of each half. Because the triangles in your circle are similar to the 30-60-90 triangle above, you can set up a proportion. The hypotenuse of our triangle is 6 (the radius of the circle) so it is set over 2 (the hypotenuse of our model 30-60-90 triangle). Half of the chord of the circle is the leg of the triangle that is across from the 60 degree angle (120/2), so it corresponds to the  side of the model triangle. 

Therefore, 

Because x is equal to half of the chord, the answer is .

The formula for the area of a circle is , and the formula for circumference is . If we solve for C in terms of r, we get
.

We can then substitute this value of r into the formula for the area:

Set the area of the circle equal to four times the circumference πr² = 4(2πr). 

Cross out both π symbols and one r on each side leaves you with r = 4(2) so r = 8 and therefore d = 16.

The perimeter of a circle = 2 πr = πd

Therefore d = 36