All PSAT Math Resources
Example Questions
Example Question #271 : Plane Geometry
Eric is riding a Ferris wheel. The Ferris wheel has 18 compartments, numbered in order clockwise. If compartment 1 is at 0 degrees and Eric enters compartment 13, what angle is he at?
180
240
260
300
280
240
12 compartments further means 240 more degrees. 240 is the answer.
360/12 = 240 degrees
Example Question #1 : How To Find The Angle Of A Sector
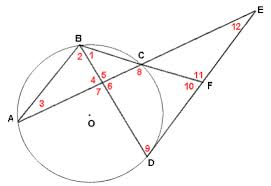
In the figure above that includes Circle O, the measure of angle BAC is equal to 35 degrees, the measure of angle FBD is equal to 40 degrees, and the measure of arc AD is twice the measure of arc AB. Which of the following is the measure of angle CEF? The figure is not necessarily drawn to scale, and the red numbers are used to mark the angles, not represent angle measures.
The measure of angle CEF is going to be equal to half of the difference between the measures two arcs that it intercepts, namely arcs AD and CD.
Thus, we need to find the measure of arcs AD and CD. Let's look at the information given and determine how it can help us figure out the measures of arcs AD and CD.
Angle BAC is an inscribed angle, which means that its meausre is one-half of the measure of the arc that it incercepts, which is arc BC.
Thus, since angle BAC is 35 degrees, the measure of arc BC must be 70 degrees.
We can use a similar strategy to find the measure of arc CD, which is the arc intercepted by the inscribed angle FBD.
Because angle FBD has a measure of 40 degrees, the measure of arc CD must be 80 degrees.
We have the measures of arcs BC and CD. But we still need the measure of arc AD. We can use the last piece of information given, along with our knowledge about the sum of the arcs of a circle, to determine the measure of arc AD.
We are told that the measure of arc AD is twice the measure of arc AB. We also know that the sum of the measures of arcs AD, AB, CD, and BC must be 360 degrees, because there are 360 degrees in a full circle.
Because AD = 2AB, we can substitute 2AB for AD.
This means the measure of arc AB is 70 degrees, and the measure of arc AD is 2(70) = 140 degrees.
Now, we have all the information we need to find the measure of angle CEF, which is equal to half the difference between the measure of arcs AD and CD.
Example Question #2 : How To Find The Angle Of A Sector
The length of an arc, 





The circumference of the circle is 
The length of the arc S is 
A ratio can be established:
Solving for 
Note: This makes sense. Since the arc S was one-fourth the circumference of the circle, the central angle formed by arc S should be one-fourth the total degrees of a circle.
Example Question #331 : Psat Mathematics

Note: Figure NOT drawn to scale.
In the above circle, 
A 



which simplifies to

Example Question #11 : Plane Geometry

Note: Figure NOT drawn to scale.
Refer to the above figure. The ratio of the area of the white sector to that of the gray sector is 5 to 1. Evaluate 
The ratio of the areas is 5 to 1, so the white sector is one sixth of the circle. This means that the central angle of the white sector is one sixth of 
Example Question #331 : Geometry

Note: Figure NOT drawn to scale.
The area of the gray sector in the above circle is 


The total area of the circle is the sum of the areas of the white and gray sectors, or
The gray sector takes up

of the circle, so the degree measure of the gray sector 
Example Question #1 : How To Find The Angle Of A Sector

Note: Figure NOT drawn to scale.
In the above circle, the length of arc 




The circumference of the circle is the sum of the lengths of the arcs 


of the circle, and its degree measure 
Example Question #22 : Circles
In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?
90
80
100
40
cannot be determined
40
Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.
Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.
Example Question #1 : How To Find The Angle Of A Sector
What is the angle of a sector of area 


To begin, you should compute the complete area of the circle:
For your data, this is:
Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:
Now, multiply this by the total 
Rounded, this is 
Example Question #1 : How To Find The Angle Of A Sector
What is the angle of a sector that has an arc length of 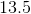



The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:
For your data, this means,
Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:
Rounded to the nearest hundredth, this is 
Certified Tutor
All PSAT Math Resources