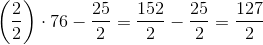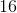PSAT Math : PSAT Mathematics
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #1641 : Psat Mathematics
Solve:
First reduce the fraction. We can divide both the numerator and the denominator by 3.
Now our expression looks like this:
When you add or subtract fractions, you need to have the same denominator. The lowest common deonminator here is 2. So we need to multiply and solve:
Example Question #1 : Whole And Part
Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?
$2.50
$6.50
$1.00
$4.00
$10.00
$2.50
If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.
Example Question #1 : Whole And Part
A certain ball that is dropped will bounce back to 3/5 of the height it was initially dropped from. If after the 2nd bounce the ball reaches 39.96 ft, what was the initial height the ball was dropped from?
100 ft
66 ft
111 ft
135 ft
150 ft
111 ft
We know the height of the initial bounce, so work backwards to find the initial height. 39.96/0.6 = 66.6 = height of ball after first bounce
66.6/0.6 = 111 ft
Example Question #122 : Fractions
A pitcher of water is filled 
30
45
40
50
35
45
If 
Example Question #1642 : Psat Mathematics
If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
Example Question #1 : How To Find The Whole From The Part
A certain bakery makes chocolate, vanilla, red velvet, and carrot cupcakes in a ratio of 2:3:5:1. If that bakery makes 63 vanilla cupcakes in one day, what is the total number of cupcakes that the bakery made that day?
Because the bakery makes 63 vanilla cupcakes in one day, start by dividing the 63 by the vanilla part of the ratio, which is 3. 
Now add up the parts of your ratio: 
Example Question #6 : Whole And Part
A circle is divided into various sized slices. One slice has an interior angle of 
In order to find the circumference of the cirlce, we will need to find the radius of the circle. We know that a slice with a 40-degree angle has an area of 
Multiply 
The area of the circle is 
The radius of the circle is 9. Use the formula for circumference to find the circumference of the circle:
The circumference of the circle is 
Example Question #1 : How To Find The Part From The Whole
If a TV show is 45 minutes long, what fraction of the show is completed 5 minutes after it begins?
1/10
1/9
1/2
1/4
1/3
1/9
5 minutes out of 45 have been completed. We can represent this as a fraction: 5/45. When simplified, this yields 1/9.
Example Question #111 : Fractions
A birthday cake is cut into 8 pieces. On the first night three pieces are eaten. On the second night, 20% of the remaining cake was eaten. On the third night, half of the remaining cake was eaten. How many slices were left to eat on the fourth night?
1/2
1
3
2
4.5
2
First night: 8 – 3 = 5 remaining.
Second night: 20% of 5 remaining = .2 * 5 = 1 slice Therefore 4 remaining.
Third night: ½ of the 4 remaining = ½*4 = 2 slices remaining
Example Question #2 : Whole And Part
There was a malfunction at a candy factory and the machines only put red, purple, and green candy into the bags. If 1/4 of the candies were red and 3/8 were green, how many purple candies were in the bag, if each bag can hold 16 pieces?
4
10
6
8
3
6
Since 1/4 of the 16 are red: 16 * 1/4 = 4 red candies. With 3/8 being green:
16 X 3/8 = 6 green candies. 16 – 4 – 6 = 6 candies remain, which must be purple.
Certified Tutor
All PSAT Math Resources
