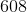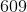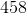If Brad can walk 3600 feet in 10 minutes, then he can walk 3600/10 = 360 feet per minute, and 360/60 = 6 feet per second.

There are 3 feet in a yard, so Brad can walk 6/3 = 2 yards per second, or 2 x 10 = 20 yards in 10 seconds.

The simplest way to handle this question is to consider the sequence as being a set of 3 repeating terms, (3,2,4). Within the first 18 terms in the sequence, this pattern will repeat a total of 6 times.

The sum of one repeat is:

Since there are 6 repeats, take the sum of one repeat (9) and multiply by the number of repeats:

The sum of the first 18 terms is 54.

Shortcut:  If you add up al the integers from  to , the sum is zero because

the positives and negatives all cancel out.  Start with the next number:

We start by multiplying 6 times 46, since the first 4 terms are already listed. We then add the product, 276, to the last listed term, 20. This gives us our answer of 296.

All answers in the sequence must end in a 5 or a 0.

Let a₁ represent the first term of the sequence and a_n represent the nth term.

We are told that each term is two greater than the term that precedes it. Thus, we can say that:

a₂ = a₁ + 2

a₃ = a₁ + 2 + 2 = a₁ + 2(2)

a₄ = a₁ + 3(2)

a₅ = a₁ + 4(2)

a_n = a₁ + (n-1)(2)

The problem tells us that the sum of the first five terms is equal to the difference between the fifth and first terms. Let's write an expression for the sum of the first five terms.

sum = a₁ + (a₁ + 2) + (a₁ + 2(2)) + (a₁ + 3(2)) + (a₁ + 4(2))

= 5a₁ + 2 + 4 + 6 + 8

= 5a₁ + 20

Next, we want to write an expression for the difference between the fifth and first terms.

a₅ - a₁ = a₁ + 4(2) – a₁ = 8

Now, we set the two expressions equal and solve for a₁.

5a₁ + 20 = 8

Subtract 20 from both sides.

5a₁ = –12

a₁ = –2.4.

The question ultimately asks us for the tenth term of the sequence. Now, that we  have the first term, we can find the tenth term.

a₁₀ = a₁ + (10 – 1)(2)

a₁₀ = –2.4 + 9(2)

= 15.6

The answer is 15.6 .

Let a₁ be the first term in the sequence. We can use the fact that a_n+1 = (a_n)² – 1 in order to find expressions for the second and third terms of the sequence in terms of a₁.

a₂ = (a₁)² – 1

a₃ = (a₂)² – 1 = ((a₁)² – 1)² – 1

We can use the fact that, in general, (a – b)² = a² – 2ab + b² in order to simplify the expression for a₃.

a₃ = ((a₁)² – 1)² – 1

= (a₁)⁴ – 2(a₁)² + 1 – 1 = (a₁)⁴ – 2(a₁)²

We are told that the third term is equal to the square of the first term. 

a₃ = (a₁)²

We can substitute (a₁)⁴ – 2(a₁)² for a₃.

(a₁)⁴ – 2(a₁)² = (a₁)²

Subtract (a₁)² from both sides.

(a₁)⁴ – 3(a₁)² = 0

Factor out (a₁)² from both terms.

(a₁)² ((a₁)² – 3) = 0

This means that either (a₁)² = 0, or (a₁)² – 3 = 0. 

If (a₁)² = 0, then a₁ must be 0. However, we are told that all the terms of the sequence are positive. Therefore, the first term can't be 0.

Next, let's solve (a₁)² – 3 = 0.

Add 3 to both sides.

(a₁)² = 3

Take the square root of both sides. 

a₁ = ±√3

However, since all the terms are positive, the only possible value for a₁ is √3.

Now, that we know that a₁ = √3, we can find a₂, a₃, and a₄.

a₂ = (a₁)² – 1 = (√3)² – 1 = 3 – 1 = 2

a₃ = (a₂)² – 1 = 2² – 1 = 4 – 1 = 3

a₄ = (a₃)² – 1 = 3² – 1 = 9 – 1 = 8

The question ultimately asks for the product of the a₂, a₃, and a₄, which would be equal to 2(3)(8), or 48.

The answer is 48.

The fourth term is: 3(23) – 1 = 69 – 1 = 68.

The fifth term is: 3(68) – 1 = 204 – 1 = 203.

The sixth term is: 3(203) – 1 = 609 – 1 = 608.

Each number in the sequence in 7 more than the number preceding it.

The equation for the terms in an arithmetic sequence is a_n = a₁ + d(n-1), where d is the difference.

The formula for the terms in this sequence is therefore a_n = 2 + 7(n-1). 

Plug in 8 for n to find the 8^th term: 

a₈ = 2 + 7(8-1) = 51

The difference between the second and fourth terms of an arithmetic sequence is twice the common difference - or, equivalently, the common difference is half the difference between the second and fourth terms.

The common difference can be subtracted from the second term to obtain the first term: