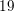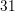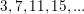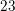PSAT Math : Sequences
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Nth Term Of An Arithmetic Sequence
A sequence of numbers is represented by the equation 
Take the equation that represents the 
The value of the 9th term is 747.
Example Question #1 : Nth Term Of An Arithmetic Sequence
You are given a sequence with the same difference between consecutive terms. We know it starts at 
From the given information, we know 
Example Question #33 : Sequences
Each term in the sequence is one less than twice the previous term.
So, 
Example Question #802 : Arithmetic
What is the next number in the following series: 0, 3, 8, 15, 24 . . . ?
40
32
35
41
37
35
The series is defined by n2 – 1 starting at n = 1. The sixth number in the series then equal to 62 – 1 = 35.
Example Question #21 : Arithmetic Sequences
A sequence of numbers is as follows:
What is the sum of the first seven numbers in the sequence?
490
621
1529
719
248
621
The pattern of the sequence is (x+1) * 2.
We have the first 5 terms, so we need terms 6 and 7:
(78+1) * 2 = 158
(158+1) * 2 = 318
3 + 8 + 18 +38 + 78 + 158 + 318 = 621
Example Question #391 : Arithmetic
Find the 
Notice that in the sequence
each term increases by 
It is always good strategy when attempting to find a pattern in a sequence to examine the difference between each term.
We continue the pattern to find:
The 
The 
The 
It is useful to note that the sequence is defined by,
where n is the number of any one term.
We can solve
to find the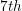 
Certified Tutor
All PSAT Math Resources
