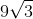The answer is 12. In this circumstance, the area of the triangle cannot be smaller than its hypotenuse length, and cannot be bigger than its hypotenuse squared (that would be the area of a square).

Drawing a quick sketch of this triangle will reveal that it is a right triangle. The lines AB and AC form the height and base of this triangle interchangeably, depending on how you look at it.

Either way the formula for the area of the triangle is the distance from A to B multiplied by the distance from A to C, divided by 2.

This is 

The area of a triangle is denoted by the equation 1/2 b x h.

b stands for the length of the base, and h stands for the height.

Here we are told that the perimeter (total length of all three sides) is 12, and the hypotenuse (the side that is neither the height nor the base) is 5 units long.

So, 12-5 = 7 for the total perimeter of the base and height.

7 does not divide cleanly by two, but it does break down into 3 and 4,

and 1/2 (3x4) yields 6.

Another way to solve this would be if you recall your rules for right triangles, one of the very basic ones is the 3,4,5 triangle, which is exactly what we have here

We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.

The base is equal to 6.

The height of an quilateral triangle is equal to , where is the length of the base.

The area of a triangle is half the product of its base and its height.

The area of  is

The area of  is

Therefore,  is  of .

Note that actually finding the measure of  is not necessary.

, and the right angles are  and , so we have two right triangles with congruent legs.

If we also know that , then the hypotenuses of the right triangles are also congruent, and this sets up the conditions of the Hypotenuse-Leg Theorem.

If we also know that , then, along with the fact that  (both being right angles) and nonincluded sides , the conditions of the Angle-Angle-Side Theorem are set up.

If we also know  and  have the same area, we can demonstrate that the other legs are congruent. The area of a right triangle is half the product of its legs, and since we have the same areas,

Since ,

The legs and the included angles (the right angles) are congruent, thus setting up the conditions for the Angle-Side-Angle Postulate. 

In all three cases, congruence follows, so the correct response is "Any of the three statements is enough to prove congruence."

We know that the sum of all the angles must be 180 and we already know one angle is 90, leaving the sum of x and y to be 90.

Solve for x to find y.

One third of 21 is 7. Four less than  7 is 3. So if angle x is 3 then that leaves 87 for angle y.

The first thing to notice is that this is a 30^o:60^o:90^o triangle. If you draw a diagram, it is easier to see that the angle that is asked for corresponds to the side with a length of 4. This will be the smallest angle. The correct answer is 30.

In the figure above, angle ADB is a right angle. Because side AC is a straight line, angle CDB must also be a right angle.

Let’s examine triangle ADB. The sum of the measures of the three angles must be 180 degrees, and we know that angle ADB must be 90 degrees, since it is a right angle. We can now set up the following equation.

x + y + 90 = 180

Subtract 90 from both sides.

x + y = 90

Next, we will look at triangle CDB. We know that angle CDB is also 90 degrees, so we will write the following equation:

y – 10 + 2x – 20 + 90 = 180

y + 2x + 60 = 180

Subtract 60 from both sides.

 y + 2x = 120

We have a system of equations consisting of x + y = 90 and y + 2x = 120. We can solve this system by solving one equation in terms of x and then substituting this value into the second equation. Let’s solve for y in the equation x + y = 90.

x + y = 90

Subtract x from both sides.

y = 90 – x

Next, we can substitute 90 – x into the equation y + 2x = 120.

(90 – x) + 2x = 120

90 + x = 120

x = 120 – 90 = 30

x = 30

Since y = 90 – x, y = 90 – 30 = 60.

The question ultimately asks us to find the positive difference between the measures of ACB and CBD. The measure of ACB = 2x – 20 = 2(30) – 20 = 40 degrees. The measure of CBD = y – 10 = 60 – 10 = 50 degrees. The positive difference between 50 degrees and 40 degrees is 10. 

The answer is 10.