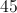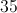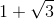Angle FHI is the supplement of angle FHG, which is an interior angle in the octagon. When two angles are supplementary, their sum is equal to 180 degrees. If we can find the measure of each interior angle in the octagon, then we can find the supplement of angle FHG, which will give us the measure of angle FHI.

The sum of the interior angles in a regular polygon is given by the formula 180(n – 2), where n is the number of sides in the polygon. An octagon has eight sides, so the sum of the angles of the octagon is 180(8 – 2) = 180(6) = 1080 degrees. Because the octagon is regular, all of its sides and angles are congruent. Thus, the measure of each angle is equal to the sum of its angles divided by 8. Therefore, each angle in the polygon has a measure of 1080/8 = 135 degrees. This means that angle FHG has a measure of 135 degrees.

Now that we know the measure of angle FHG, we can find the measure of FHI. The sum of the measures of FHG and FHI must be 180 degrees, because the two angles form a line and are supplementary. We can write the following equation:

Measure of FHG + measure of FHI = 180

135 + measure of FHI = 180

Subtract 135 from both sides.

Measure of FHI = 45 degrees.

The answer is 45. 

An octagon contains six triangles, or 1080 degrees. This means with 8 angles, each angle is 135 degrees.

There are 360 degrees and 8 angles, so dividing leaves 45 degrees per angle.

By angle addition, 

 is an angle of a reguar pentagon, so its measure is .

To find , first we find .

By angle addition, 

 is an angle of a regular pentagon and has measure .

, as an angle of an equilateral triangle, has measure . 

 is equilateral, so ; Pentagon  is regular, so . Therefore, , and by the Isosceles Triangle Theorem, .

The degree measures of three angles of a triangle total , so:

Since

we have 

The figure described is below.

Each of the angles of the pentagon has measure 

 is an isosceles triangle, and , so 

and

Since

,

and by the parallel postulate,

Quadrilateral  has exactly one pair of parallel sides, so it is a trapezoid. 

IF you draw the longest diagonal across the shape, the length of it is 13.4. This means the radius must be at least 6.7. The answer is 7.

To get the expression equivalent to the perimeter, add the lengths of the sides:

Since the perimeter is 190, we can simplify this to

and solve as follows:

To get the expression equivalent to the perimeter, add the lengths of the sides:

Since the perimeter is 225, we can simplify this to

and, furthermore, since ,

The trick is to construct segments perpendicular to  from  and , calling the points of intersection  and  respectively.

Each interior angle of a regular octagon measures

,

and by symmetry,  ,

so .

This makes  and   triangles.

Since their hypotenuses are sides of the octagon with length 1, then their legs - in particular,  and  - have length . 

Also, since a rectangle was formed when the perpendiculars were drawn, .

The length of diagonal  is

.

The trick is to construct segments perpendicular to  from  and , calling the points of intersection  and  respectively.

Each interior angle of a regular dodecagon measures

.

Since  and  are perpendicular to , it can be shown via symmetry that they are also perpendicular to . Therefore, 

 and  both measure  

and  and  are  triangles with long legs  and . Since their hypotenuses are sides of the dodecagon and therefore have length 1, 

.

Also, since Quadrilateral  is a rectangle, .

The length of diagonal  is.