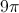Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Geometry

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Cylinders

A water glass has the shape of a right cylinder. The glass has an interior radius of 2 inches, and a height of 6 inches. The glass is 75% full. What is the volume of the water in the glass (in cubic inches)?

Possible Answers:

$9 \pi$

$36 \pi$

$12 \pi$

$18 \pi$

$24 \pi$

Correct answer:

$18 \pi$

Explanation:

The volume of a right cylinder with radius r=2 and height h=6 is:

$\pi r^2 h = \pi (2)^2 (6) = 24 \pi$

Since the glass is only 75% full, only 75% of the interior volume of the glass is occupied by water. Therefore the volume of the water is:

$24 \pi \times ( 75 / 100 ) = 24 \pi (0.75) = 18 \pi$

Report an Error

Example Question #14 : Cylinders

A circle has a circumference of $4\pi$ and it is used as the base of a cylinder. The cylinder has a surface area of $16\pi$ . Find the volume of the cylinder.

Possible Answers:

$6\pi$

$8\pi$

$4\pi$

$2\pi$

$10\pi$

Correct answer:

$8\pi$

Explanation:

Using the circumference, we can find the radius of the circle. The equation for the circumference is $2\pi r$ ; therefore, the radius is 2.

Now we can find the area of the circle using $\pi r^{2}$ . The area is $4\pi$ .

Finally, the surface area consists of the area of two circles and the area of the mid-section of the cylinder: $2\cdot 4\pi +4\pi h=16\pi$ , where $h$ is the height of the cylinder.

Thus, $h=2$ and the volume of the cylinder is $4\pi h=4\pi \cdot 2=8\pi$ .

Report an Error

Example Question #831 : Sat Mathematics

A metal cylindrical brick has a height of $6\ in$ . The area of the top is $25\pi\ in^2$ . A circular hole with a radius of $2\ in$ is centered and drilled half-way down the brick. What is the volume of the resulting shape?

Possible Answers:

$125\pi\ in^3$

$150\pi\ in^3$

$138\pi\ in^3$

$175\pi\ in^3$

$100\pi\ in^3$

Correct answer:

$138\pi\ in^3$

Explanation:

To find the final volume, we will need to subtract the volume of the hole from the total initial volume of the cylinder.

The volume of a cylinder is given by the product of the base area times the height: $V=A_{base}h$ .

Find the initial volume using the given base area and height.

$V_i=(25\pi)(6)=150\pi\ in^3$

Next, find the volume of the hole that was drilled. The base area of this cylinder can be calculated from the radius of the hole. Remember that the height of the hole is only half the height of the block.

$V_{hole}=(\pi r^2)h$

$V_{hole}=(\pi(2)^2)(3)=(4\pi)(3)=12\pi\ in^3$

Finally, subtract the volume of the hole from the total initial volume.

$150\pi-12\pi=138\pi\ in^3$

Report an Error

Example Question #14 : How To Find The Volume Of A Cylinder

What is the volume of a cylinder with a diameter of 13 inches and a height of 27.5 inches?

Possible Answers:

$381.44\pi \ in^{3}$

$357.5\pi \ in^{3}$

$2583.1\pi \ in^{3}$

$4647.5\ in^{3}$

$1161.88\pi \ in^{3}$

Correct answer:

$1161.88\pi \ in^{3}$

Explanation:

The equation for the volume of a cylinder is V = Ah, where A is the area of the base and h is the height.

Thus, the volume can also be expressed as V = πr²h.

The diameter is 13 inches, so the radius is 13/2 = 6.5 inches.

Now we can easily calculate the volume:

V = 6.5²π * 27.5 = 1161.88π in³

Report an Error

Example Question #311 : Geometry

A water tank takes the shape of a closed cylinder whose exterior has height 40 feet and a base with radius 12 feet; the tank is six inches thick throughout. To the nearest hundred, how many cubic feet of water does the tank hold?

Possible Answers:

$14,800 \textrm{ ft}^{3}$

$16,200 \textrm{ ft}^{3}$

$5,200 \textrm{ ft}^{3}$

$3,700 \textrm{ ft}^{3}$

$16,400 \textrm{ ft}^{3}$

Correct answer:

$16,200 \textrm{ ft}^{3}$

Explanation:

Six inches is equal to 0.5 feet, so the height of the interior of the tank is

$40 - 2 \times 0.5 = 39$ feet;

the radius of the base of the interior of the tank is

12 - 0.5 = 11.5 feet.

The amount of water the tank holds is the volume of the interior of the tank, which is

$V = \pi r^{2}h$

$V \approx 3.14 \cdot 11.5^{2} \cdot 39 \approx 16, 195$ cubic feet.

This rounds to 16,200.

Report an Error

Example Question #22 : How To Find The Volume Of A Cylinder

Barrel

The above diagram is one of a cylindrical tub. The company wants to make a cylindrical tub with four times the volume, but whose base is only three times the radius. How high should this new tub be?

Possible Answers:

$53\frac{1}{3} \textup{ in}$

$30 \textup{ in}$

$22\frac{1}{2} \textup{ in}$

$17 \frac{7}{9} \textup{ in}$

$90 \textup{ in}$

Correct answer:

$17 \frac{7}{9} \textup{ in}$

Explanation:

The volume of the given tub can be expressed using the following formula, setting r = 25 and h= 40 ,

$V = \pi r^{2} h$

$V = \pi \cdot 25^{2} \cdot 40$

$V = 25,000 \pi$ cubic inches.

The new tub should have four times this volume, or

$V = 25,000 \pi \cdot 4 = 100,000 \pi$ cubic inches.

The radius is to be three times that of the above tub, which will be

$r = 25 \cdot 3 = 75$ inches.

The height can therefore be calculated as follows:

$\pi r^{2} h = V$

$\pi \cdot75 ^{2} \cdot h = 100,000 \pi$

$5,625\pi h = 100,000\pi$

$h = \frac{100,000 \pi}{5,625 \pi} = 17 \frac{7}{9}$ inches

Report an Error

Example Question #24 : How To Find The Volume Of A Cylinder

Barrel

The above diagram is one of a cylindrical tub. The tub is holding water at 70% capacity. To the nearest cubic foot, how much more water can it hold?

Possible Answers:

$38 \textup{ ft}^{3}$

$9 \textup{ ft}^{3}$

$29 \textup{ ft}^{3}$

$23 \textup{ ft}^{3}$

$14 \textup{ ft}^{3}$

Correct answer:

$14 \textup{ ft}^{3}$

Explanation:

The volume of the cylinder can be calculated using the following formula, setting r = 25 and h= 40 ,

$V = \pi r^{2} h$

$V \approx 3.14 \cdot 25^{2} \cdot 40 \approx 78,539.8$ cubic inches.

The tub is 70% full, so it is 30% empty; it can hold

$78,539.8 \times 0.30 \approx 23,561.7$ more cubic inches of water.

The problem asks for the number of cubic feet, so divide by the cube of 12, or 1,728:

$23,561.7 \div 1,728 \approx 13.6$

The correct response is 14 cubic feet.

Report an Error

Example Question #25 : How To Find The Volume Of A Cylinder

$\textup{A cylindrical container with a diameter of 4 cm and a height of 16 cm}$

$\textup{is filled half full with water. What is the volume of the water in the glass?}$

Possible Answers:

$96\pi \: \textup{ cm}^{3}$

$32\pi \: \textup{ cm}^{3}$

$144\pi \: \textup{ cm}^{3}$

$48\pi \: \textup{ cm}^{3}$

$64\pi \: \textup{ cm}^{3}$

Correct answer:

$32\pi \: \textup{ cm}^{3}$

Explanation:

$\textup{Volume}= \pi r^{2}h\; \; \; \;r=2, h = 8 \textup{ (only half full)}$

$\textup{V}=2^{2}\cdot 8\pi \: \: \: \: \: \textup{V}=32\pi$

Report an Error

Example Question #21 : Cylinders

Two cylinders are full of milk. The first cylinder is 9” tall and has a base diameter of 3”. The second cylinder is 9” tall and has a base diameter of 4”. If you are going to pour both cylinders of milk into a single cylinder with a base diameter of 6”, how tall must that cylinder be for the milk to fill it to the top?

Possible Answers:

12"

6.25"

30"

Correct answer:

6.25"

Explanation:

Volume of cylinder = π * (base radius)² x height = π * (base diameter / 2 )² x height

Volume Cylinder 1 = π * (3 / 2 )² x 9 = π * (1.5 )² x 9 = π * 20.25

Volume Cylinder 2 = π * (4 / 2 )² x 9 = π * (2 )² x 9 = π * 36

Total Volume = π * 20.25 + π * 36

Volume of Cylinder 3 = π * (6 / 2 )² x H = π * (3 )² x H = π * 9 x H

Set Total Volume equal to the Volume of Cylinder 3 and solve for H

π * 20.25 + π * 36 = π * 9 x H

20.25 + 36 = 9 x H

H = (20.25 + 36) / 9 = 6.25”

Report an Error

Example Question #1 : How To Find The Length Of An Arc

Figure not drawn to scale.

In the figure above, circle C has a radius of 18, and the measure of angle ACB is equal to 100°. What is the perimeter of the red shaded region?

Possible Answers:

36 + 10π

18 + 36π

36 + 20π

36 + 36π

18 + 10π

Correct answer:

36 + 10π

Explanation:

The perimeter of any region is the total distance around its boundaries. The perimeter of the shaded region consists of the two straight line segments, AC and BC, as well as the arc AB. In order to find the perimeter of the whole region, we must add the lengths of AC, BC, and the arc AB.

The lengths of AC and BC are both going to be equal to the length of the radius, which is 18. Thus, the perimeter of AC and BC together is 36.

Lastly, we must find the length of arc AB and add it to 36 to get the whole perimeter of the region.

Angle ACB is a central angle, and it intercepts arc AB. The length of AB is going to equal a certain portion of the circumference. This portion will be equal to the ratio of the measure of angle ACB to the measure of the total degrees in the circle. There are 360 degrees in any circle. The ratio of the angle ACB to 360 degrees will be 100/360 = 5/18. Thus, the length of the arc AB will be 5/18 of the circumference of the circle, which equals 2πr, according to the formula for circumference.

length of arc AB = (5/18)(2πr) = (5/18)(2π(18)) = 10π.

Thus, the length of arc AB is 10π.

The total length of the perimeter is thus 36 + 10π.

The answer is 36 + 10π.

Report an Error

View PSAT Mathematics Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View PSAT Mathematics Tutors

Shakeel
Certified Tutor

View PSAT Mathematics Tutors

Darian
Certified Tutor

University of North Texas, Current Undergrad Student, English.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Chicago, LSAT Tutors in Los Angeles, ISEE Tutors in Seattle, ACT Tutors in Chicago, Math Tutors in New York City, Statistics Tutors in Denver, French Tutors in Seattle, ACT Tutors in Philadelphia, Computer Science Tutors in Philadelphia, Math Tutors in Washington DC

Popular Courses & Classes

ISEE Courses & Classes in Miami, ACT Courses & Classes in Washington DC, Spanish Courses & Classes in Boston, ACT Courses & Classes in Boston, LSAT Courses & Classes in San Diego, Spanish Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Miami, Spanish Courses & Classes in Chicago, SSAT Courses & Classes in Philadelphia, ACT Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in Los Angeles, SSAT Test Prep in New York City, ACT Test Prep in Denver, SSAT Test Prep in San Diego, MCAT Test Prep in Denver, GMAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Phoenix, ACT Test Prep in Boston, ACT Test Prep in Dallas Fort Worth, ISEE Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Geometry

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : Cylinders

Example Question #14 : Cylinders

Example Question #831 : Sat Mathematics

Example Question #14 : How To Find The Volume Of A Cylinder

Example Question #311 : Geometry

Example Question #22 : How To Find The Volume Of A Cylinder

Example Question #24 : How To Find The Volume Of A Cylinder

Example Question #25 : How To Find The Volume Of A Cylinder

Example Question #21 : Cylinders

Example Question #1 : How To Find The Length Of An Arc

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: