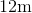Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Geometry

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Surface Area Of A Sphere

A sphere is perfectly contained within a cube that has a surface area of 726 square units. In square units, what is the surface area of the sphere?

Possible Answers:

484π

None of the other answers

30.25π

11π

121π

Correct answer:

121π

Explanation:

To begin, we must determine the dimensions of the cube. To do this, recall that the surface area of a cube is made up of six squares and is thus defined as: A = 6s², where s is one of the sides of the cube. For our data, this gives us:

726 = 6s²; 121 = s²; s = 11

Now, if the sphere is contained within the cube, that means that 11 represents the diameter of the sphere. Therefore, the radius of the sphere is 5.5 units. The surface area of a sphere is defined as: A = 4πr². For our data, that would be:

A = 4π * 5.5² = 30.25 * 4 * π = 121π

Report an Error

Example Question #3 : How To Find The Surface Area Of A Sphere

The area of a circle with radius 4 divided by the surface area of a sphere with radius 2 is equal to:

Possible Answers:

0.5

Correct answer:

Explanation:

The surface area of a sphere is 4πr². The area of a circle is πr². 16/16 is equal to 1.

Report an Error

Example Question #13 : Spheres

What is the ratio of the surface area of a cube to the surface area of a sphere inscribed within it?

Possible Answers:

6/π

2π

π/3

3/π

4/π

Correct answer:

6/π

Explanation:

Let's call the radius of the sphere r. The formula for the surface area of a sphere (A) is given below:

A = 4πr²

Because the sphere is inscribed inside the cube, the diameter of the sphere is equal to the side length of the cube. Because the diameter is twice the length of the radius, the diameter of the sphere is 2r. This means that the side length of the cube is also 2r.

The surface area for a cube is given by the following formula, where s represents the length of each side of the cube:

surface area of cube = 6s²

The formula for surface area of a cube comes from the fact that each face of the cube has an area of s², and there are 6 faces total on a cube.

Since we already determined that the side length of the cube is the same as 2r, we can replace s with 2r.

surface area of cube = 6(2r)²= 6(2r)(2r) = 24r².

We are asked to find the ratio of the surface area of the cube to the surface area of the sphere. This means we must divide the surface area of the cube by the surface area of the sphere.

ratio = (24r²)/(4πr²)

The r²term cancels in the numerator and denominator. Also, 24/4 simplifes to 6.

ratio = (24r²)/(4πr²) = 6/π

The answer is 6/π.

Report an Error

Example Question #191 : Geometry

What is the surface area of a hemisphere with a diameter of $4\ cm$ ?

Possible Answers:

$20\pi \ cm^{2}$

$12\pi \ cm^{2}$

$8\pi \ cm^{2}$

$16\pi \ cm^{2}$

$18\pi \ cm^{2}$

Correct answer:

$12\pi \ cm^{2}$

Explanation:

A hemisphere is half of a sphere. The surface area is broken into two parts: the spherical part and the circular base.

The surface area of a sphere is given by $SA = 4\pi r^{2}$ .

So the surface area of the spherical part of a hemisphere is $SA = 2\pi r^{2}$ .

The area of the circular base is given by $A = \pi r^{2}$ . The radius to use is half the diameter, or 2 cm.

Report an Error

Example Question #191 : Psat Mathematics

If a sphere has an approximate volume of $904.32\textup{ cubic meters}$ , then what is the approximate diameter of this sphere?

Possible Answers:

$17\textup{m}$

$9\textup{m}$

$12\textup{m}$

$10\textup{m}$

$15\textup{m}$

Correct answer:

$12\textup{m}$

Explanation:

The formula for the volume of a sphere is

$v=\left ( \frac{4}{3} \right )\pi r^3$

Therefore,

$904.32=\left ( \frac{4}{3} \right )\pi r^3$

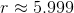
Dividing both sides by $\left ( \frac{4}{3} \right )\pi$ , leaves us with $r^3\approx215.89$ . Taking the cube root, we find $r\approx5.999$ , meaning our diameter $d\approx12$ .

Report an Error

Example Question #1 : How To Find The Radius Of A Sphere

A cube with volume 27 cubic inches is inscribed inside a sphere such that each vertex of the cube touches the sphere. What is the radius, in inches, of the sphere?

Possible Answers:

√3/2 (approximately 1.73)

(3√3)/2 (approximately 2.60)

8.5

Correct answer:

(3√3)/2 (approximately 2.60)

Explanation:

We know that the cube has a volume of 27 cubic inches, so each side of the cube must be ∛27=3 inches. Since the cube is inscribed inside the sphere, the diameter of the sphere is the diagonal length of the cube, so the radius of the sphere is half of the diagonal length of the cube. To find the diagonal length of the cube, we use the distance formula d=√(3²+3²+3² )=√(3*3² )=3√3, and then divide the result by 2 to find the radius of the sphere, (3√3)/2.

Report an Error

Example Question #1 : How To Find The Radius Of A Sphere

The surface area of a sphere is 100π square feet. What is the radius in feet?

Possible Answers:

100

Correct answer:

Explanation:

S = 4π(r²)

100π = 4π(r²)

100 = 4r²

25 = r²

5 = r

Report an Error

Example Question #1 : How To Find The Radius Of A Sphere

A spherical water tank has a surface area of 400 square meters. To the nearest tenth of a meter, give the radius of the tank.

Possible Answers:

$11.3\textup{ m}$

$5.6\textup{ m}$

$9.1\textup{ m}$

$4.6\textup{ m}$

$3.2\textup{ m}$

Correct answer:

$5.6\textup{ m}$

Explanation:

Given radius , the surface area of a sphere is given by the formula

$S = 4 \pi r^{2}$

Set S = 400 and solve for :

$4 \pi r^{2} = 400$

$4 \pi r^{2}\div 4 = 400 \div 4$

$\pi r^{2} = 100$

$\pi r^{2} \div \pi = 100 \div \pi$

$r^{2} \approx 100 \div 3.14159 \approx 31.831$

$r \approx \sqrt{31.831} \approx 5.6$ meters.

Report an Error

Example Question #4 : How To Find The Radius Of A Sphere

A spherical tank is to hold 50,000 liters of water. Given that one cubic meter is equal to 1,000 liters, give the radius of this tank to the nearest tenth of a meter.

Possible Answers:

$2.3\textup{ m}$

$3.5\textup{ m}$

$4.0 \textup{ m}$

$4.6\textup{ m}$

$2.0 \textup{ m}$

Correct answer:

$2.3\textup{ m}$

Explanation:

Given radius , the volume of a sphere is given by the formula

$V = \frac{4}{3} \pi r^{3}$

Since 1,000 liters = 1 cubic meter, 50,000 liters = 50 cubic meters, and we find by setting V= 50 :

$\frac{4}{3} \pi r^{3} = 50$

$\frac{3}{4} \cdot \frac{4}{3} \pi r^{3} = \frac{3}{4} \cdot 50$

$\pi r^{3} = 37.5$

$r^{3} =\frac{ 37.5}{\pi} \approx 11.9366$

$r \approx\sqrt[3]{ 11.9366} \approx 2.3$ meters.

Report an Error

Example Question #4 : How To Find The Radius Of A Sphere

The Kelvin temperature scale is basically the same as the Celsius scale except with a different zero point; to convert degrees Celsius to Kelvins, add 273. Also, by Charles's law, the volume of a given mass of gas varies directly as its temperature, expressed in Kelvins.

In the early morning, when the temperature is $5^{\circ }C$ , a spherical balloon is filled with helium until its radius is 100 meters. At 2:00 PM, the temperature is $20^{\circ }C$ . To the nearest tenth of a meter, what is the radius of the balloon at this time?

Possible Answers:

$98.3 \textup{ m}$

$107.2\textup{ m}$

$101.8 \textup{ m}$

$63.0\textup{ m}$

$158.7 \textup{ m}$

Correct answer:

$101.8 \textup{ m}$

Explanation:

The volume of the balloon is given by the formula

$V = \frac{4}{3} \pi r^{3}$ .

Also, by the variation relationship,

$\frac{V'}{T'} = \frac{V}{T}$

We do not need to calculate the original volume of the balloon; we can simply replace the volume with the formula:

$\frac{ \frac{4}{3} \pi r'^{3}}{T'} = \frac{ \frac{4}{3} \pi r^{3}}{T}$

Dividing both sides by $\frac{4}{3} \pi$ yields a new equation:

$\frac{ r'^{3}}{T'} = \frac{ r^{3}}{T}$

The initial radius is r = 100

The initial temperature is $T = 273 + 5 = 278 \textup{ K}$

The final (noon) temperature is $T ' = 273 + 20= 293 \textup{ K}$

Substitute to find the final radius:

$\frac{ r'^{3}}{293} = \frac{ 100^{3}}{278}$

$r'^{3} = \frac{ 1,000,000}{278} \cdot 293 \approx 1,053,957$

$r' = \approx\sqrt[3]{ 1,053,957} \approx 101.8$ meters.

Report an Error

View PSAT Mathematics Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View PSAT Mathematics Tutors

Kelly
Certified Tutor

Rhode Island College, Bachelors, History/Political Science. Rhode Island College, Masters, History.

View PSAT Mathematics Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Houston, French Tutors in Boston, Statistics Tutors in Denver, GRE Tutors in Atlanta, Physics Tutors in Los Angeles, GMAT Tutors in Boston, GRE Tutors in Boston, Computer Science Tutors in Chicago, French Tutors in Atlanta, ACT Tutors in Washington DC

Popular Courses & Classes

SAT Courses & Classes in Houston, Spanish Courses & Classes in New York City, GRE Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in New York City, SAT Courses & Classes in Chicago, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in San Diego, SAT Courses & Classes in Washington DC, SSAT Courses & Classes in Seattle, SAT Courses & Classes in Boston

Popular Test Prep

GRE Test Prep in Los Angeles, SAT Test Prep in Phoenix, SAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, LSAT Test Prep in Chicago, ACT Test Prep in Washington DC, MCAT Test Prep in Boston, MCAT Test Prep in Seattle, SSAT Test Prep in Seattle, GRE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Geometry

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #2 : How To Find The Surface Area Of A Sphere

Example Question #3 : How To Find The Surface Area Of A Sphere

Example Question #13 : Spheres

Example Question #191 : Geometry

Example Question #191 : Psat Mathematics

Example Question #1 : How To Find The Radius Of A Sphere

Example Question #1 : How To Find The Radius Of A Sphere

Example Question #1 : How To Find The Radius Of A Sphere

Example Question #4 : How To Find The Radius Of A Sphere

Example Question #4 : How To Find The Radius Of A Sphere

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: