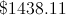All PSAT Math Resources
Example Questions
Example Question #1 : How To Find Simple Interest
Dan took out a $1200 loan at a rate of 3% simple interest a year. What is the amount of interest accrued for one month?
$1200 is the amount that he took out.
3% annually would yield an interest amount of $36.
Therefore, each month, he would be paying $3 a month.
Example Question #2 : How To Find Simple Interest
Peter wanted to buy a car and borrowed $2,500 from the bank at 5% simple interest per year. He was able to pay back the loan in one lump sum at six months. What was the total amount he paid the bank?
Simple interest is given by 




Remember, six months is the same as half of a year. The total paid back to the bank is the principle plus the interest, or $2,562.50.
Example Question #3 : How To Find Simple Interest
I have $100 in my bank. After one year, I have withdrawn a total of $20 and I still have $85 in the bank. What is the yearly interest rate of my bank account?
Since I have withdrawn $20, that means I only have $80 in my account.

which is 6.25%.
Example Question #4 : How To Find Simple Interest
You really want to buy a car that costs $15,000 but you only have $5,000 saved. Rather than getting a bank loan, your parents offer to lend you the extra money but will require you to pay them back with 4.3% interest. How much will car cost in total after you have paid your parents back?
Amount borrowed = $15,000 – $5,000 = $10,000
Interest of 4.3% = $10,000 * 0.043 = $430
Total cost of car = $5000 + $10000 + $430 = $15,430
Example Question #41 : Monetary Percentage
Ted works over the summer and makes $9 per hour. He works for 20 hours each week for 10 weeks. After paying 10% in taxes, he buys a bike for $500 and puts the rest of his money in the bank.
If Ted's bank pays 5% interest on the total sum once per year, and Ted doesn't add or remove anything from the account, how much money (rounded to the nearest cent) will Ted have in 5 years?
To start, we see that Ted works for 20 hours per week for 10 weeks. This means he works a total of 200 hours over the summer. He is paid $9 dollars each hour. Therefore he makes $9 x 200 hours = $1800 total over the summer. He then has to pay 10% in taxes, or .1 x $1800, leaving him with 
Now we have to find out how much he will have 5 years later. Since the bank pays 5% interest each year, we know that he will make 5% of what he has each year. He starts with $1,120. 5% of this value is 
This is also the same as multiplying instead by 1.05. We repeat this step 5 times, giving us:
Example Question #42 : Monetary Percentage
Jane borrows 


Use the simple interest formula:
Interest equals the initial amount multiplied by the annual interest rate multiplied by the number of years:
Let 
Let 
Let 
Let 
Therefore:
Example Question #1 : Percent Of Change
At a certain store, prices for all items were assigned in January. Each month after that, the price was 20% less than the price the previous month. If the price of an item was x dollars in January, approximately what was the price in dollars of the item in June?
0.51x
0.81x
0.33x
0.66x
0.12x
0.33x
The question tells us that the price in January was x. To find the price in February, we decrease the price of x by 20%, which is the same as taking 80% of x. (In general, a P% decrease of a number is the same as (100 – P)% times that number). Continue to take 0.8 times the previous month's price to find the next month's price until we have the price for June, as follows:
January Price: x
February Price: 0.8 * January Price = 0.8x
March Price: 0.8 * February Price = 0.8 * 0.8x = 0.82 * x
April Price: 0.8 * March Price = 0.8 * 0.8 * 0.8x = 0.83 * x
May Price: 0.8 * April Price = 0.8 * 0.8 * 0.8 * 0.8x = 0.84 * x
June Price: 0.8 * May Price = 0.8 * 0.8 * 0.8 * 0.8 * 0.8x = 0.85 * x; therefore, the price in June was 0.85 ≈ 0.328 ≈ 0.33 times the original price.
Example Question #1 : Percent Of Change
The sale of a tablet decreased from $500 to $450. By what percentage did the cost decrease?
10%
5%
15%
20%
1%
10%
Set up the following ratio
50/500 = n/100
The cost of the tablet decreased by $50. The original cost is $500; therefore, 50 is the numerator and 500 is the denominator on the left side of the ratio.
Since a percentage is a part of a whole, n symbolizes the the percentage decrease.
To solve for n, you can cross multiply. So, 50(100) = n(500).
n = 10%
Example Question #1 : Percent Of Change
On Monday, the price of a shirt costs x dollars. On Tuesday, the manager puts the shirt on sale for 10% off Monday's price. On Wednesday, the manager increases the price of the shirt by 10% of Tuesday's price. Describe the change in price from Monday to Wednesday.
10% increase
1% increase
No change
10% decrease
1% decrease
1% decrease
To find the cost on Tuesday, take 10% off Monday's price. In other words, find 90% of Monday's price. This is simply 0.9x. If we are to now add 10% of this value back onto itself to find Wednesday's price, we want 100% + 10%, or 110% of 0.9x.
1.1(0.9x) = 0.99x
This value is 1% smaller than x.
Example Question #44 : Percentage
If the length of a rectangle is increased by thirty percent, which of the following most closely approximates the percent by which the rectangle's width must decrease, so that the area of the rectangle remains unchanged?
30
17
21
23
25
23
All PSAT Math Resources