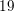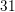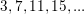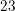PSAT Math : Arithmetic
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Next Term In An Arithmetic Sequence
Each term in the sequence is one less than twice the previous term.
So, 
Example Question #2 : How To Find The Next Term In An Arithmetic Sequence
What is the next number in the following series: 0, 3, 8, 15, 24 . . . ?
37
40
32
41
35
35
The series is defined by n2 – 1 starting at n = 1. The sixth number in the series then equal to 62 – 1 = 35.
Example Question #1 : How To Find The Next Term In An Arithmetic Sequence
A sequence of numbers is as follows:
What is the sum of the first seven numbers in the sequence?
1529
490
248
719
621
621
The pattern of the sequence is (x+1) * 2.
We have the first 5 terms, so we need terms 6 and 7:
(78+1) * 2 = 158
(158+1) * 2 = 318
3 + 8 + 18 +38 + 78 + 158 + 318 = 621
Example Question #391 : Arithmetic
Find the 
Notice that in the sequence
each term increases by 
It is always good strategy when attempting to find a pattern in a sequence to examine the difference between each term.
We continue the pattern to find:
The 
The 
The 
It is useful to note that the sequence is defined by,
where n is the number of any one term.
We can solve
to find the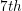 
Example Question #1 : How To Find The Sale Price
Maria was shopping for a camera and found one that was on sale for 30% off. As she went to pay for it, the store announced an instant sale that took an additional 10% off all items. If the final price Maria paid was $207.27, what was the original price (before all discounts) of the camera?
$767.67
$82.91
$329.00
$518.18
$290.18
$329.00
To reconstruct an original price from a sale price, use:
Original Price – Original Price * Mark-down-percent = Sale Price, or
Original Price * (1 - Mark-down-percent) = Sale Price
To do a double mark-down problem, we must do this twice. For the 10%:
Original Sale Price * (1 – 10%) = $207.27
Original Sale Price = $207.27/0.9 = $230.30.
For the pre-all-discount price,
Original Price * (1 – 30%) = $230.30
Original Price = $230.30/0.7 = $329.00.
Example Question #1 : How To Find The Sale Price
An mp3 player costs $100 on day one. On day two, the shop owner decides to decrease the price by 10% of the day one price. However, on day three the owner changes her mind and raises the price by 10% of the day two price. What is the new price of the mp3 player?
$99
$101
$100
$102
$98
$99
10% of the day one price = 0.1(100) = $10.
Therefore the day two price = 100 - 10 = $90.
10% of the day two price = 0.1(90) = $9.
Therefore the day three price = 90 + 9 = $99.
Example Question #3 : How To Find The Sale Price
The price of a purse is reduced by 20%. It is then put on final sale with an additional 30% off. What is the total discount on the purse?
56%
50%
48%
40%
44%
44%
Let us assume that the original purse is $100. The price after the first reduction is $80. After the second reduction the price is now $56. The difference between 100 and 56 is 44, giving 44% off.
Example Question #1 : How To Find The Sale Price
A store is having a sale. If you buy one widget for the regular price of $20, you can buy a second widget for 40% off the regular price. How much per widget does a customer save by buying two widgets during the sale instead of buying two widgets at the regular price?
8
12
32
4
20
4
Widget 1 costs $20.
Widget 2 is on sale for 40%($20) off, or $8 off, or $20 – $8 = $12.
Two widgets during the sale cost $20 + $12 = $32.
Two widgets at regular price cost $20 + $20 = $40.
The total amount saved during the sale is $40 – $32 = $8.
This is the savings for two widgets, so the savings for one widget is $8/2 = $4.
Example Question #4 : How To Find The Sale Price
A $225 dress goes on sale for 75% off. It is then discounted again for 10% off. How much money was saved on by the final purchase?
50.63
16.88
33.75
174.37
191.25
174.37
The answer is $174.37.
The dress originally cost $225 but when it went on sale for 75% off we multiply the sale cost by 0.75. We see that through the sale we save $168.75 makeing the new cost of the dress $56.25.
Now we take the new cost of the dress ($56.25) and multiply that by 0.10 to represent the 10% discount. From this we see we save an additional $5.63 making the final cost of the dress $50.63.
The total savings on the dress sum up to $174.37.
Example Question #1 : How To Find The Sale Price
A stove is regularly priced for $300. What is the difference one would pay when buying it at a 20% discount rather than a 10% discount, with an additional 10% discount off the sale price?
$30
$5
$3
$20
$3
Buying the stove at a 20% discount would be $240. If one buys it at a sale of 10%, with another 10% off then the price would be $243, so the difference is $3
20% of 300 is 0.2 * 300 = 60 → 300 – 60 = 240
10% of 300 is 0.1 * 300 = 30 → 300 – 30 = 270
10% of 270 is 0.1 * 270 = 27 → 270 – 27 = 243
243 – 240 = 3
All PSAT Math Resources
