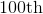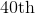PSAT Math : Arithmetic
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #2 : Basic Operations
What property of arithmetic is demonstrated here?
Symmetric
Associative
Transitive
Commutative
Associative
The symbols express the idea that if three numbers are multiplied, the same product results regardless of which numbers are multiplied first. This is the associative property of multiplication.
Example Question #3 : How To Multiply Integers
Multiply in modulo 8:
None of the other responses is correct.
In modulo 8 arithmetic, a number is congruent to the remainder of its division by 8.
and
so
making the correct response.
Example Question #1 : How To Add Integers
My sister invited me to play an online word game. In the game vowels (a,e,i,o,u) are worth 3 points and consonants are worth 5. How much would I score if I use the word “University” ?
42
63
45
30
42
In the word we have 4 vowels (3 x 4 = 12 points) and 6 consonants (5 x 6= 30). If we add the points together we get a total of 42 points.
Example Question #321 : Arithmetic
What is the sum of multiples of 10 from 10 to 140 inclusive?
Listing them all, 10-20-30-40-50-60-70-80-90-100-110-120-130-140 you see you can divide the numbers in half (7 pairs). Alternatively you can take (140-10+10)/2/10, adding that additional +10 in the numerator because it is inclusive, giving you 7. Just adding the top and bottom numbers gives you 10+140 for 150. 150*7 is 1050.
Example Question #1 : How To Add Integers
What number replaces the circle in the following sequence?
The sequence is formed by starting with 1 and adding successive powers of 5. The numbers are obtained as follows:
Example Question #2 : How To Add Integers
Suppose you know the values of the variables in the expression
and you wish to evaluate it.
Which operation do you execute last?
Division
Addition
Subtraction
Multiplication
Squaring
Addition
In the absence of grouping symbols, the first operations that should be carried out are exponentiations, followed by multiplications and divisions, followed by additions and subtractions.
The additions and subtractions are carried out from left to right. Since the addition is the one to the right, it is performed last.
Example Question #3 : How To Add Integers
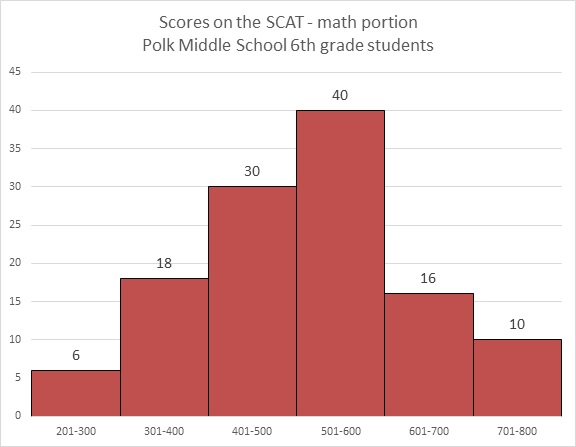
Refer to the above graph. Francie, a sixth grader at Polk, scored a 372 on the math portion of the SCAT. Which of the following could have been her rank among the students?
By scoring a 372, Francie was outcored by all of the students who finished in the 401-800 ranges, which add up to:
She was outscored by at most an additional 17 students (the other 17 in the 301-400 range), for a total of at most
Francie finished between 97th and 114th place, making 100th place the only possible choice.
Example Question #1712 : Sat Mathematics
Mark has 5 pants and 7 shirts in his closet. He wants to wear a different pant/shirt combination each day without buying new clothes for as long as he can. How many weeks can he do this for?
6
4
8
5
7
5
The fundamental counting principle says that if you want to determine the number of ways that two independent events can happen, multiply the number of ways each event can happen together. In this case, there are 5 * 7, or 35 unique combinations of pants & shirts Mark can wear. If he wears one combination each day, he can last 35 days, or 5 weeks, without buying new clothes.
Example Question #1 : Permutation / Combination
Twenty students enter a contest at school. The contest offers a first, second, and third prize. How many different combinations of 1st, 2nd, and 3rd place winners can there be?
400
20
6840
8000
4620
6840
This is a permutation problem, because we are looking for the number of groups of winners. Consider the three positions, and how many choices there are for each position: There are 20 choices for 1st place, 19 for 2nd place, and 18 for 3rd place.
20, 19, 18
Multiply to get 6840.
Example Question #2 : Permutation / Combination
A baker has four different types of frosting, three different kinds of sprinkles, and 8 different cookie cutters. How many different cookie combinations can the baker create if each cookie has one type of frosting and one type of sprinkle?
15
24
96
48
96
Since this a combination problem and we want to know how many different ways the cookies can be created we can solve this using the Fundamental counting principle. 4 x 3 x 8 = 96
Multiplying each of the possible choices together.
All PSAT Math Resources
