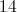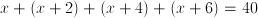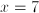Customers must choose a salad, an entree, and a dessert. There are three different salads, four entrees, and two desserts.

The simplest way of determining the number of combinations is by multiplying the number of options for each part of the meal. In other words, we can find the product of 3, 4, and 2, which would give us 24.

Sometimes, if you can't think of a way to mathetimatically determine all of the different combinations of something, it helps to write out as many as you can. Let's write out all of the possible cominbations just to verify that there are 24. Let's call the different salads S1, S2, and S3. We will call the four entrees E1, E2, E3, and E4, and we will call the desserts D1 and D2.

Here are the possible lunch special combinations:

S1, E1, D1

S1, E1, D2

S1, E2, D1

S1, E2, D2

S1, E3, D1

S1, E3, D2

S1, E4, D1

S1, E4, D2

S2, E1, D1

S2, E1, D2

S2, E2, D1

S2, E2, D2

S2, E3, D1

S2, E3, D2

S2, E4, D1

S2, E4, D2

S3, E1, D1

S3, E1, D2

S3, E2, D1

S3, E2, D2

S3, E3, D1

S3, E3, D2

S3, E4, D1

S3, E4, D2

The answer is 24.

There are five possible choices for the first space. For the second there are four possible, three for the third, and two for the fourth. 5 * 4 * 3 * 2 = 120 possible arrangements.

The first three characters must be distinct letters, none of which are 'I' or 'O', meaning that three letters will be selected from a set of 24. Also, order will be important, so the number of ways to choose this group of three will be .

The letters are followed by either a '1' or a '2', so this makes 2 possibilities.

The next three characters will be numerals, and there will be no restrictions, so the number of ways to choose this group will be .

By the multiplication principle, the number of ways to choose an employee number will be

The first three characters must be distinct letters, meaning that three letters will be selected from a set of 26. Also, order will be important, so the number of ways to choose this group of three will be .

The next four characters will be numerals, with no restrictions, so the number of ways to choose this group will be 

The last character can be any of 26 letters.

By the multiplication principle, the number of ways to choose an employee number will be

The first two characters must be distinct letters, meaning that two letters will be selected from a set of 26. Also, order will be important, so the number of ways to choose this group of two will be .

Similarly, since the last two characters will be chosen according to the same rule, with repetition allowed between the two groups, there will be  ways to choose them as well.

The next four characters will be numerals, but there will be no restrictions, so the number of ways to choose this group will be .

By the multiplication principle, the number of ways to choose an employee number will be

There will be 15 gaps of  long but 16 tick marks because there will be a tick mark on each end of the ruler.

A prime numbers is a number greater than 1 that can only be divided by 1 and itself. Simply count from 1 to 25 and see how many values fit the criteria.

2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25

Prime numbers are underlined. Nine prime numbers are in this set interval.

Let x equal the smallest of the four numbers. Therefore:

Therefore the four odd numbers are 7, 9, 11, and 13. Since all are prime except 9, three of the numbers are prime.

To find the median of a set of numbers, we must first order them from smallest to greatest.

Next, we must find the number directly in the middle, which has an equal number of numbers to the right and to the left.

Therefore, our answer is .