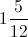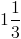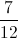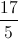Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Arithmetic

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find A Solution To A Compound Fraction

Simplify:

$\frac{\frac{3}{4}-\frac{2}{5}}{2- \frac{9}{10}}$

Possible Answers:

$\frac{7}{22}$

$\frac{77}{200}$

$\frac{147}{200}$

$\frac{5}{72}$

$\frac{7}{38}$

Correct answer:

$\frac{7}{22}$

Explanation:

$\frac{\frac{3}{4}-\frac{2}{5}}{2- \frac{9}{10}}$

$= \left ( \frac{3}{4}-\frac{2}{5} \right ) \div \left ( 2- \frac{9}{10} \right )$

$= \left ( \frac{15}{20}-\frac{8}{20} \right ) \div \left ( \frac{20}{10}- \frac{9}{10} \right )$

$= \frac{7}{20} \div \frac{11}{10}$

$= \frac{7}{20} \cdot \frac{10}{11}$

$= \frac{7}{2} \cdot \frac{1}{11}$

$= \frac{7}{22}$

Report an Error

Example Question #3 : How To Find A Solution To A Compound Fraction

Simplify:

$\frac{1-\frac{1}{4}}{1-\frac{1}{8}}$

Possible Answers:

$\frac{21}{32}$

$\frac{6}{7}$

$\frac{8}{9}$

$\frac{1}{2}$

$\frac{7}{8}$

Correct answer:

$\frac{6}{7}$

Explanation:

$\frac{1-\frac{1}{4}}{1-\frac{1}{8}}$

$= \left (1 -\frac{1}{4} \right ) \div \left (1-\frac{1}{8} \right )$

$= \left (\frac{4}{4}-\frac{1}{4} \right ) \div \left (\frac{8}{8}-\frac{1}{8} \right )$

$= \frac{3}{4} \div \frac{7}{8}$

$= \frac{3}{4} \cdot \frac{8}{7}$

$= \frac{3}{1} \cdot \frac{2}{7}$

$= \frac{6}{7}$

Report an Error

Example Question #2 : How To Find A Solution To A Compound Fraction

Simplify:

$\frac{2-\frac{1}{4}}{1+\frac{1}{7}}$

Possible Answers:

$1 \frac{17}{32}$

None of the other responses gives the correct answer.

$1\frac{1}{28}$

$1\frac{27}{28}$

Correct answer:

$1 \frac{17}{32}$

Explanation:

$\frac{2-\frac{1}{4}}{1+\frac{1}{7}}$

$= \left ( 2-\frac{1}{4} \right ) \div \left ( 1+\frac{1}{7} \right )$

$= \left (\frac{8}{4}-\frac{1}{4} \right ) \div \left ( \frac{7}{7}+\frac{1}{7} \right )$

$= \frac{7}{4} \div \frac{8}{7}$

$= \frac{7}{4} \cdot \frac{7}{8}$

$= \frac{49}{32}$

$= 1 \frac{17}{32}$

Report an Error

Example Question #6 : General Fractions

Simplify:

$\frac{\frac{1}{3}+\frac{4}{5} }{\frac{2}{3}+\frac{4}{5} }$

Possible Answers:

$\frac{1}{2}$

$\frac{17} {22}$

$\frac{2}{9}$

$\frac{374}{225}$

$\frac{5}{8}$

Correct answer:

$\frac{17} {22}$

Explanation:

$\frac{\frac{1}{3}+\frac{4}{5} }{\frac{2}{3}+\frac{4}{5} }$

$=\left ( \frac{1}{3}+\frac{4}{5} \right ) \div\left ( \frac{2}{3}+\frac{4}{5} \right )$

$=\left ( \frac{5}{15}+\frac{12}{15} \right ) \div\left ( \frac{10}{15}+\frac{12}{15} \right )$

$= \frac{17}{15} \div \frac{22}{15}$

$= \frac{17}{15} \cdot \frac{15}{22}$

$= \frac{17}{1} \cdot \frac{1}{22}$

$= \frac{17} {22}$

Report an Error

Example Question #3 : How To Find A Solution To A Compound Fraction

Simplify:

$\frac{\frac{1}{2}-\frac{1}{10} }{\frac{1}{4}-\frac{1}{5} }$

Possible Answers:

$\frac{1}{50}$

$\frac{1}{2}$

The correct answer is not given among the other responses.

Correct answer:

The correct answer is not given among the other responses.

Explanation:

$\frac{\frac{1}{2}-\frac{1}{10} }{\frac{1}{4}-\frac{1}{5} }$

$= \left ( \frac{1}{2}-\frac{1}{10} \right )\div \left ( \frac{1}{4}-\frac{1}{5} \right )$

$= \left ( \frac{5}{10}-\frac{1}{10} \right )\div \left ( \frac{5}{20}-\frac{4}{20} \right )$

$= \frac{4}{10} \div \frac{1}{20}$

$= \frac{4}{10} \cdot \frac{20}{1}$

$= \frac{4}{1} \cdot \frac{2}{1}$

$= \frac{8}{1} = 8$

This answer is not among the given choices.

Report an Error

Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction

To make 48 cookies you need 1 cup white sugar, 1 cup packed brown sugar and 3 cups of flour. You want to make 12 cookies, so you adjust the ingredients accordingly. After the adjustment, how many total cups of dry ingredients do you have?

Possible Answers:

¹/₄ c

1 ¹/₂ c

1 ¹/₄ c

³/₄ c

1 ³/₄ c

Correct answer:

1 ¹/₄ c

Explanation:

Going from 48 cookies to 12 cookies is a scaling factor of ¹/₄, so all the ingredients get multiplied by ¹/₄. In order to make 12 cookies you will need ¹/₄ c white sugar, 1/4 c packed brown sugar, and ³/₄ c flour. Added all together you get ⁵/₄ or 1 ¹/₄ c.

Report an Error

Example Question #2 : How To Find Out A Mixed Fraction From An Improper Fraction

What is $\frac{17}{12}$ written as a mixed number?

Possible Answers:

$2\frac{1}{6}$

$\frac{7}{12}$

$1\frac{1}{3}$

$1\frac{5}{12}$

$3\frac{1}{2}$

Correct answer:

$1\frac{5}{12}$

Explanation:

How many times does 12 go into 17? Once with a remainder of 5.

So $\frac{17}{12}$ becomes $1\frac{5}{12}$

Report an Error

Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction

If 3x=20 , what does equal?

Possible Answers:

$8\tfrac{1}{3}$

$6\tfrac{1}{3}$

$7\tfrac{2}{3}$

$7\tfrac{1}{3}$

$6\tfrac{2}{3}$

Correct answer:

$6\tfrac{2}{3}$

Explanation:

First, you must solve the equation for . Then, you must convert the answer's improper fraction to a mixed fraction.

3x=2

Solve for .

$x = \frac{20}{3}$

Now, to convert an improper fraction, you must see how many times the denominator goes into the numerator, and then leave the remainder as a fraction. Example below:

Find out how many times the denominator goes into the numerator:

$20\div3 = 6, remainder 2$

Therefore,

$x = 6\tfrac{2}{3}$

Report an Error

Example Question #1 : How To Find Out An Improper Fraction From A Mixed Fraction

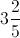
What is $3\frac{2}{5}$ as an improper fraction?

Possible Answers:

$\frac{21}{5}$

$\frac{11}{5}$

$\frac{10}{2}$

$\frac{17}{5}$

$\frac{6}{2}$

Correct answer:

$\frac{17}{5}$

Explanation:

$3\frac{2}{5}$ becomes $3 + \frac{2}{5} = \frac{15}{5} + \frac{2}{5} = \frac{17}{5}$

Report an Error

Example Question #1 : How To Find The Amount Of Rational Numbers Between Two Numbers

Two numbers have a greatest common divisor of 4 and a least common multiple of 40. How many different pairs of numbers are there that satisfy these properties?

Possible Answers:

$Infinitely\ many$

Correct answer:

Explanation:

The greatest common divisor is 4. This means that both numbers must be divisible by 4. Furthermore, the least common multiple is 40, so both must divide 40.

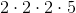
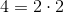
The prime factorization of 40 is $2\cdot 2\cdot 2\cdot 5$ . For a number to divide 40, it must therefore be composed of (at most) three 2's and one 5. Because $4=2\cdot 2$ divides both numbers, we also know that they must both have at least two 2's.

Now each number will have either two or three 2's and zero or one 5's. However, we also know that they can't both have three 2's, (since then the greatest common divisor would have three 2's as well). Similarly, only one can have a 5.

In essence, our problem becomes one of choice. We have 2 places with value 4. We choose to give a 5 to one of the two. We then give a 2 to one of the two. If we give a 5 and a 2 to the same side, we end up with $5\cdot 2\cdot 4=40$ and 4. If we give a 5 to one and a 2 to the other, we end up with $5\cdot 4=20$ and $2\cdot 4=8$ .

Thus our two pairs are:

4,40 and 8,20

Report an Error

View PSAT Mathematics Tutors

Michael
Certified Tutor

University of Massachusetts Amherst, Bachelor in Arts, Political Science and Government. University of Massachusetts Amherst,...

View PSAT Mathematics Tutors

Crony
Certified Tutor

Brown University, Bachelor of Science, Neuroscience.

View PSAT Mathematics Tutors

Bagher
Certified Tutor

San Jose State University, Master's/Graduate, Physics.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Chicago, Computer Science Tutors in New York City, English Tutors in Houston, French Tutors in Seattle, Math Tutors in Miami, English Tutors in New York City, MCAT Tutors in Seattle, GRE Tutors in Boston, Biology Tutors in Denver, Spanish Tutors in Atlanta

Popular Courses & Classes

ISEE Courses & Classes in Miami, MCAT Courses & Classes in Chicago, GRE Courses & Classes in San Diego, GMAT Courses & Classes in San Diego, SSAT Courses & Classes in Miami, GMAT Courses & Classes in Boston, ACT Courses & Classes in New York City, GMAT Courses & Classes in Houston, GRE Courses & Classes in Philadelphia, LSAT Courses & Classes in Miami

Popular Test Prep

SSAT Test Prep in Seattle, ISEE Test Prep in Miami, GRE Test Prep in Houston, LSAT Test Prep in San Diego, ISEE Test Prep in Washington DC, LSAT Test Prep in Los Angeles, GMAT Test Prep in Seattle, GMAT Test Prep in Miami, ACT Test Prep in Dallas Fort Worth, GMAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Arithmetic

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : How To Find A Solution To A Compound Fraction

Example Question #3 : How To Find A Solution To A Compound Fraction

Example Question #2 : How To Find A Solution To A Compound Fraction

Example Question #6 : General Fractions

Example Question #3 : How To Find A Solution To A Compound Fraction

Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction

Example Question #2 : How To Find Out A Mixed Fraction From An Improper Fraction

Example Question #1 : How To Find Out A Mixed Fraction From An Improper Fraction

Example Question #1 : How To Find Out An Improper Fraction From A Mixed Fraction

Example Question #1 : How To Find The Amount Of Rational Numbers Between Two Numbers

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: