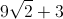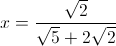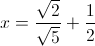Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Basic Squaring / Square Roots

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Add Square Roots

Simplify the expression:

$\sqrt{45} + \sqrt{125} + \sqrt{175}$

Possible Answers:

The expression cannot be siimplified further.

$5 \sqrt{3} + 5 \sqrt{ 5}+5 \sqrt{ 7}$

$15 \sqrt{5}$

$5 \sqrt{3} + 12 \sqrt{ 5}$

$8 \sqrt{ 5}+5 \sqrt{ 7}$

Correct answer:

$8 \sqrt{ 5}+5 \sqrt{ 7}$

Explanation:

For each of the expressions, factor out a perfect square:

$\sqrt{45} + \sqrt{125} + \sqrt{175}$

$= \sqrt{9 \cdot 5} + \sqrt{25 \cdot 5} + \sqrt{25 \cdot 7}$

$= \sqrt{9 } \cdot \sqrt{ 5} + \sqrt{25 } \cdot \sqrt{ 5}+ \sqrt{25} \cdot \sqrt{ 7}$

$=3 \sqrt{ 5} +5 \sqrt{ 5}+5 \sqrt{ 7}$

$=\left (3 +5 \right ) \sqrt{ 5}+5 \sqrt{ 7}$

$=8 \sqrt{ 5}+5 \sqrt{ 7}$

Report an Error

Example Question #2 : How To Add Square Roots

Simplify:

$\sqrt{54} - \sqrt{24} + \sqrt{6}$

Possible Answers:

$2 \sqrt{6}$

The expression cannot be simplified further.

$4\sqrt{6}$

$6 \sqrt{6}$

Correct answer:

$2 \sqrt{6}$

Explanation:

Simplify each of the radicals by factoring out a perfect square:

$\sqrt{54} - \sqrt{24} + \sqrt{6}$

$= \sqrt{9 \cdot 6} - \sqrt{4\cdot 6} + \sqrt{6}$

$= \sqrt{9} \cdot \sqrt{6} - \sqrt{4} \cdot \sqrt{6} + \sqrt{6}$

$= 3\sqrt{6} - 2 \sqrt{6} + 1\sqrt{6}$

$=\left ( 3 - 2 + 1 \right ) \sqrt{6}$

$= 2 \sqrt{6}$

Report an Error

Example Question #3 : How To Add Square Roots

Add the square roots into one term:

$\small {\sqrt{12}} + {\sqrt{75}}$

Possible Answers:

None of the other answers

$\small 5{\sqrt{3}}$

$\small 6{\sqrt{3}}$

$\small 7{\sqrt{3}}$

$\small \small 8{\sqrt{3}}$

Correct answer:

$\small 7{\sqrt{3}}$

Explanation:

In order to solve this problem we need to simplfy each of the radicals. By doing this we will get two terms that have the same number under the radical which will allow us to combine the terms.

$\small {\sqrt{12}} + {\sqrt{75}}$

$\small = \small {\sqrt{4}} \times {\sqrt{3}} + {\sqrt{25}} \times {\sqrt{3}}$

$\small \small = 2 {\sqrt{3}} + 5 {\sqrt{3}}$

$\small = 7 {\sqrt{3}}$

Report an Error

Example Question #3 : How To Add Square Roots

Simplify:

$\sqrt{2}+\sqrt{2}+\sqrt{3}+3\sqrt{5}$

Possible Answers:

$2\sqrt{2}+6\sqrt{5}$

$6\sqrt{10}$

$2\sqrt{2}+\sqrt{3}+3\sqrt{5}$

$3\sqrt{6}+3\sqrt{5}$

$6\sqrt{30}$

Correct answer:

$2\sqrt{2}+\sqrt{3}+3\sqrt{5}$

Explanation:

Remember that you treat square roots like you do variables in the sense that you just add the like factors. In this problem, the only set of like factors is the pair of $\sqrt{2}$ values. Hence:

$\sqrt{2}+\sqrt{2}+\sqrt{3}+3\sqrt{5} = 2\sqrt{2}+\sqrt{3}+3\sqrt{5}$

Do not try to simplify any further!

Report an Error

Example Question #4 : How To Add Square Roots

Simplify:

$\sqrt{2}+3\sqrt{12}+2\sqrt{50}+\sqrt{3}$

Possible Answers:

$18\sqrt{5}$

$\sqrt{2}+4\sqrt{3}+3\sqrt{12}$

$11\sqrt{2}+7\sqrt{3}$

$5\sqrt{2}+3\sqrt{3}$

$18\sqrt{6}$

Correct answer:

$11\sqrt{2}+7\sqrt{3}$

Explanation:

Begin by simplifying your more complex roots:

$\sqrt{12}= \sqrt{2*2*3}=2\sqrt{3}$

$\sqrt{50} = \sqrt{5*5*2}=5\sqrt{2}$

This lets us rewrite our expression:

$\sqrt{2}+3\sqrt{12}+2\sqrt{50}+\sqrt{3} = \sqrt{2}+3(2\sqrt{3})+2(5\sqrt{2})+\sqrt{3}$

Do the basic multiplications of coefficients:

$\sqrt{2}+3(2\sqrt{3})+2(5\sqrt{2})+\sqrt{3} = \sqrt{2}+6\sqrt{3}+10\sqrt{2}+\sqrt{3}$

Reorder the terms:

$\sqrt{2}+10\sqrt{2}+6\sqrt{3}+\sqrt{3}$

Finally, combine like terms:

$11\sqrt{2}+7\sqrt{3}$

Report an Error

Example Question #1 : How To Multiply Square Roots

Multiply and simplify. Assuming all integers are positive real numbers.

$2\sqrt{5}\cdot6\sqrt{20}$

Possible Answers:

120

160

Correct answer:

120

Explanation:

$2\sqrt{5}\cdot6\sqrt{20}$

Multiply the coefficents outside of the radicals.

$2\cdot6= 12$

Then multiply the radicans. Simplify by checking for a perfect square.

$\sqrt{5\cdot 20}=\sqrt{100}=10$

Final answer is your leading coefficent, , multiplied by the answer acquired by multiplying the terms under the radican, .

$12\cdot10= 120$

The final answer is 120 .

Report an Error

Example Question #11 : Basic Squaring / Square Roots

Mulitply and simplify. Assume all integers are positive real numbers.

$\sqrt{3}(3\sqrt{2}+\sqrt{3})$

Possible Answers:

$27\sqrt{2}$

$3\sqrt{6}+9$

$3\sqrt{6}+3$

$9\sqrt{2}+3$

$9\sqrt{6}$

Correct answer:

$3\sqrt{6}+3$

Explanation:

$\sqrt{3}(3\sqrt{2}+\sqrt{3})$

Order of operations, first distributing the $\sqrt{3}$ to all terms inside the parentheses.

$(1\cdot 3\sqrt{3}\cdot \sqrt{2})+(\sqrt{3}\cdot\sqrt{3})$

$3\sqrt{3\cdot 2}+\sqrt{3\cdot 3}\rightarrow3\sqrt{6}+\sqrt{9}\rightarrow3\sqrt{6}+3$

The final answer is $3\sqrt{6}+3$ .

Report an Error

Example Question #1 : How To Multiply Square Roots

The square root(s) of 36 is/are ________.

Possible Answers:

-6

6 and -6

None of these answers are correct.

6, -6, and 0

Correct answer:

6 and -6

Explanation:

To square a number is to multiply that number by itself. Because 6 x 6 = 36 AND -6 x -6 = 36, both 6 and -6 are square roots of 36.

Report an Error

Example Question #1 : How To Multiply Square Roots

Simplify:

$\sqrt{4}*\sqrt{12}*\sqrt{5}$

Possible Answers:

$\sqrt{15}$

$\sqrt{21}$

$4\sqrt{15}$

$5\sqrt{12}$

$2\sqrt{60}$

Correct answer:

$4\sqrt{15}$

Explanation:

Multiplication of square roots is easy! You just have to multiply their contents by each other. Just don't forget to put the result "under" a square root! Therefore:

$\sqrt{4}*\sqrt{12}*\sqrt{5}$

becomes

$\sqrt{4*12*5}=\sqrt{240}$

Now, you need to simplify this:

$\sqrt{240} = \sqrt{2*2*2*2*3*5}$

You can "pull out" two s. (Note, that it would be even easier to do this problem if you factor immediately instead of finding out that 4*12*5 = 240 .)

After pulling out the s, you get:

$\sqrt{2*2*2*2*3*5} = 2*2(\sqrt{3*5}) = 4\sqrt{15}$

Report an Error

Example Question #11 : Basic Squaring / Square Roots

Solve for $\dpi{100} x$ :

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Possible Answers:

$x=3$

$x=\frac{\sqrt{2}}{\sqrt{5}}+\frac{1}{2}$

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

$x=\frac{\sqrt{5}}{\sqrt{2}}+2$

$x=\sqrt{9}$

Correct answer:

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Explanation:

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Notice how all of the quantities in square roots are divisible by 9

$x\sqrt{9\times 5}+x\sqrt{9\times 8}=\sqrt{9\times 2}$

$x\sqrt{9}\sqrt{5}+x\sqrt{9}\sqrt{4\times 2}=\sqrt{9}\sqrt{2}$

$3x\sqrt{5}+3x\sqrt{4}\sqrt{2}=3\sqrt{2}$

$3x\sqrt{5}+6x\sqrt{2}=3\sqrt{2}$

$x(3\sqrt{5}+6\sqrt{2})=3\sqrt{2}$

$x=\frac{3\sqrt{2}}{3\sqrt{5}+6\sqrt{2}}$

Simplifying, this becomes

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Report an Error

View PSAT Mathematics Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View PSAT Mathematics Tutors

Germaine
Certified Tutor

Princeton University, Bachelor in Arts, Philosophy.

View PSAT Mathematics Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Washington DC, ISEE Tutors in Philadelphia, Reading Tutors in Chicago, LSAT Tutors in Miami, Biology Tutors in Boston, Algebra Tutors in Washington DC, GRE Tutors in Miami, Reading Tutors in Phoenix, French Tutors in Washington DC, SAT Tutors in Denver

Popular Courses & Classes

Spanish Courses & Classes in Atlanta, MCAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Miami, GMAT Courses & Classes in Atlanta, GMAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Philadelphia, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Boston, GMAT Courses & Classes in Chicago, Spanish Courses & Classes in San Diego

Popular Test Prep

GMAT Test Prep in Chicago, ISEE Test Prep in Miami, GMAT Test Prep in Los Angeles, SAT Test Prep in Phoenix, GRE Test Prep in Houston, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Houston, MCAT Test Prep in Houston, GMAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Basic Squaring / Square Roots

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #1 : How To Add Square Roots

Example Question #2 : How To Add Square Roots

Example Question #3 : How To Add Square Roots

Example Question #3 : How To Add Square Roots

Example Question #4 : How To Add Square Roots

Example Question #1 : How To Multiply Square Roots

Example Question #11 : Basic Squaring / Square Roots

Example Question #1 : How To Multiply Square Roots

Example Question #1 : How To Multiply Square Roots

Example Question #11 : Basic Squaring / Square Roots

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: