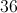All PSAT Math Resources
Example Questions
Example Question #9 : How To Multiply Complex Numbers
What is the eighth power of ?
The correct response is not given among the other choices.
First, square using the square of a binomial pattern as follows:
Raising this number to the fourth power yields the correct response:
Example Question #10 : How To Multiply Complex Numbers
What is the ninth power of ?
None of the other responses is correct.
To raise a negative number to an odd power, take the absolute value of the base to that power and give its opposite:
To raise to a power, divide the power by 4 and raise to the remainder. Since
,
Therefore,
Example Question #11 : Complex Numbers
Simplify:
Use the FOIL method that states to multiply the Firsts, Outter, Inner, Lasts. Also remember that :
Example Question #812 : Algebra
If and are positive integers and , then what is the value of ?
43 = 64
Alternatively written, this is 4(4)(4) = 64 or 43 = 641.
Thus, m = 3 and n = 1.
m/n = 3/1 = 3.
Example Question #531 : Algebra
Write the following logarithm in expanded form:
Example Question #7 : Exponents And Rational Numbers
Which of the following lists the above quantities from least to greatest?
I, IV, III, II
IV, III, II, I
I, III, II, IV
I, IV, II, III
II, III, I, IV
I, III, II, IV
Example Question #2 : Exponential Ratios And Rational Numbers
Solve for .
Since
Hence
Example Question #1 : Exponents And Rational Numbers
Simplify:
Example Question #221 : Exponents
Solve for :
From the equation one can see that
Hence must be equal to 25.
Example Question #2 : Exponents And Rational Numbers
Evaluate:
Certified Tutor
All PSAT Math Resources












![= \left [\left (1+ i \right )^{2} \right ]^{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/240868/gif.latex)



















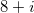


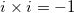

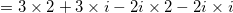














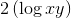















![\sqrt[3]{x^{10}y^{8}z^{9}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25511/gif.latex)


![\sqrt[3]{xy^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31988/gif.latex)
![x^{3}y^{2}z^{3}\sqrt[3]{xy^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31984/gif.latex)
![x^{3}y^{2}z^{3}^{\sqrt[3]{xyz}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31987/gif.latex)
![\sqrt[3]{x^{9}xy^{6}y^{2}z^{9}}=x^{3}y^{2}z^{3}\sqrt[3]{xy^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/109415/gif.latex)