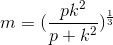PSAT Math : Algebra
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #81 : Equations / Inequalities
All of the following equations have no solution except for which one?
Since all of the equations have the same symbols save for one number, the problem is essentially as follows:
For what value of 
have a solution set other than the empty set?
We can simplify as follows:
If 
Therefore, the only equation among the given choices whose solution set is not the empty set is the equation
which is the correct choice.
Example Question #2 : How To Find Out When An Equation Has No Solution
Which of the following equations has no real solutions?
Each of the equations given in the other choices has at least one real solution.
We can examine each individually.
This equation has a solution.
This equation has a solution.
This equation has a solution.
This equation has no solution, since a fourth root of a number must be nonnegative.
The correct choice is 
Example Question #1 : Linear / Rational / Variable Equations
Solve 
No solutions
No solutions
By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.
Example Question #1 : How To Find The Solution To A Rational Equation With Lcd
1
2
–1
0
–2
2
Example Question #103 : Linear / Rational / Variable Equations
–b/(m + 1)
–b/(m2 – 1)
b/(m2 + 1)
–bm/(m2 + 1)
bm/(m2 + 1)
b/(m2 + 1)
Example Question #1 : How To Find The Solution To A Rational Equation With Lcd
In the equation below, 
Example Question #1 : Algebra
If 6x = 42 and xk = 2, what is the value of k?
1/7
1/6
7
2/7
5
2/7
Solve the first equation for x by dividing both sides of the equation by 6; the result is 7. Solve the second equation for k by dividing both sides of the equation by x, which we now know is 7. The result is 2/7.
Example Question #1 : Algebra
If 4x + 5 = 13x + 4 – x – 9, then x = ?
–5/4
0
5/4
5/8
8
5/4
Start by combining like terms.
4x + 5 = 13x + 4 – x – 9
4x + 5 = 12x – 5
–8x = –10
x = 5/4
Example Question #1 : How To Find The Solution To An Equation
If 3 – 3x < 20, which of the following could not be a value of x?
–4
–6
–3
–5
–2
–6
First we solve for x.
Subtracting 3 from both sides gives us –3x < 17.
Dividing by –3 gives us x > –17/3.
–6 is less than –17/3.
Example Question #2 : Algebra
Let x be a number. Increasing x by twenty percent yields that same result as decreasing the product of four and x by five. What is x?
The problem tells us that increasing x by twenty percent gives us the same thing that we would get if we decreased the product of four and x by five. We need to find expressions for these two situations, and then we can set them equal and solve for x.
Let's find an expression for increasing x by twenty percent. We could represent this as x + 20%x = x + 0.2x = 1.2x = 6x/5.
Let's find an expression for decreasing the product of four and x by five. First, we must find the product of four and x, which can be written as 4x. Then we must decrease this by five, so we must subtract five from 4x, which could be written as 4x - 5.
Now we must set the two expressions equal to one another.
6x/5 = 4x - 5
Subtract 6x/5 from both sides. We can rewrite 4x as 20x/5 so that it has a common denominator with 6x/5.
0 = 20x/5 - 6x/5 - 5 = 14x/5 - 5
0 = 14x/5 - 5
Now we can add five to both sides.
5 = 14x/5
Now we can multiply both sides by 5/14, which is the reciprocal of 14/5.
5(5/14) = (14x/5)(5/14) = x
25/14 = x
The answer is 25/14.
Certified Tutor
All PSAT Math Resources
