All PSAT Math Resources
Example Questions
Example Question #3 : How To Find Inverse Variation
Find the inverse of 
To find the inverse of a function we need to first switch the 


We now solve for y by subtracting 1 from each side
From here we divide both sides by 2 which results in
Example Question #611 : Algebra
Find the inverse of 
To find the inverse we first switch the variables then solve for y.
Then we subtract 
Now we divide by 






Example Question #2 : How To Find Inverse Variation
Find the inverse equation of:
To solve for an inverse, we switch x and y and solve for y. Doing so yields:
Example Question #3 : How To Find Inverse Variation
Find the inverse equation of 
1. Switch the 

2. Solve for 
Example Question #1 : Algebraic Fractions



When 

If 



If 


1. Using any of the two 

Using 
2. Use your new equation 

Example Question #1 : How To Find Inverse Variation
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
If 


An inverse variation is a function in the form: 


Substitute each 

Therefore, the constant of variation, 




Example Question #1 : How To Evaluate A Fraction
Evaluate the following equation when 
1. Plug in 

2. Perform the above operations.
Example Question #1 : How To Evaluate A Fraction
Mary walked to school at an average speed of 2 miles per hour and jogged back along the same route at an average speed of 6 miles per hour. If her total traveling time was 1 hour, what was the total number of miles in the round trip?
Since Mary traveled 3 times as quickly coming from school as she did going to school (6 miles per hour compared to 2 miles per hour), we know that Mary spent only a third of the time coming from school as she did going. If x represents the number of hours it took to get to school, then x/3 represents the number of hours it took her to return.
Knowing that the total trip took 1 hour, we have:
x + x/3 = 1
3x/3 + 1x/3 = 1
4x/3 = 1
x = 3/4
So we know it took Mary 3/4 of an hour to travel to school (and the remaining 1/4 of an hour to get back).
Remembering that distance = rate * time, the distance Mary traveled on her way to school was (2 miles per hour) * (3/4 of an hour) = 3/2 miles. Furthermore, since she took the same route coming back, she must have traveled 3/2 of a mile to return as well.
Therefore, the the total number of miles in Mary's round trip is 3/2 miles + 3/2 miles = 6/2 miles = 3 miles.
Example Question #2 : How To Evaluate A Fraction
If 

To raise 


Example Question #3 : How To Evaluate A Fraction
Solve ![]()
0
infinitely many solutions
no solution
–1
infinitely many solutions
The common denominator of the left side is x(x–1). Multiplying the top and bottom of 1/x by (x–1) yields
![]()
![]()
![]()
![]()
Since this statement is true, there are infinitely many solutions.
Certified Tutor
All PSAT Math Resources













































































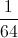


![w^\frac{2}{3}=\sqrt[3]{w^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177545/gif.latex)
![(\frac{1}{8})^\frac{2}{3}=\sqrt[3]{(\frac{1}{8})^2}=\sqrt[3]{\frac{1}{64}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177546/gif.latex)
![\sqrt[3]{\frac{1}{64}}=\frac{1}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/177547/gif.latex)




