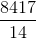Begin by simplifying the numerator.

 has a common denominator of .  Therefore, we can rewrite it as:

Now, in our original problem this is really is:

When you divide by a fraction, you really multiply by the reciprocal:

Begin by simplifying the numerator and the denominator.

Numerator

 has a common denominator of .  Therefore, we have:

Denominator

 has a common denominator of .  Therefore, we have:

Now, reconstructing our fraction, we have:

To make this division work, you multiply the numerator by the reciprocal of the denominator:

Recall that dividing is equivalent multiplying by the reciprocal.  Therefore, ((x - 4) / (1 / 2)) / (1 / (x + 4)) = ((x - 4) * 2)  *  (x + 4) / 1. 

Let's simplify this further:

(2x – 8) * (x + 4) = 2x² – 8x + 8x – 32 = 2x² – 32

Begin by isolating the variables:

Now, the common denominator of the variable terms is . The common denominator of the constant values is . Thus, you can rewrite your equation:

Simplify:

Cross-multiply:

Simplify:

Finally, solve for :

A negative exponent in the numerator of a fraction can be rewritten with a positive exponent in the denominator. The same is true for a negative exponent in the denominator. Thus, .

When is multiplied by , the numerators and denominators cancel out, and you are left with 1.

Another way to represent this question is:

In the one's column, and add to produce a number with a two in the one's place. In the ten's column, we can see that a one must carry in order to get a digit in the hundred's place. Together, we can combine these deductions to see that the sum of and must be twelve (a one in the ten's place and a two in the one's place).

In the one's column:

The one carries to the ten's column.

In the ten's column:

The three goes into the answer and the one carries to the hundred's place. The final answer is 132. From this, we can see that because .

Using this information, we can solve for .

You can check your answer by returning to the original addition and plugging in the values of and .

First we want to simplify the expression: .

One way to simplify this complex fraction is to find the least common multiple of all the denominators, i.e. the least common denominator (LCD). If we find this, then we can multiply every fraction by the LCD and thereby be left with only whole numbers. This will make more sense in a little bit.

The denominators we are dealing with are 2, 3, 4, 5, and 6. We want to find the smallest multiple that these numbers have in common. First, it will help us to notice that 6 is a multiple of both 2 and 3. Thus, if we find the least common multiple of 4, 5, and 6, it will automatically be a multiple of both 2 and 3. Let's list out the first several multiples of 4, 5, and 6.

4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60

5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60

6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60

The smallest multiple that 4, 5, and 6 have in common is 60. Thus, the least common multiple of 4, 5, and 6 is 60. This also means that the least common multiple of 2, 3, 4, 5, and 6 is 60. Therefore, the LCD of all the fractions is 60.

Let's think of the expression we want to simplify as one big fraction. The numerator contains the fractions 1/4, 1/3, and –1/5. The denominator of the fraction is 1/2, –1/6 and 1. Remember that if we have a fraction, we can multiply the numerator and denominator by the same number without changing the value of the fraction. In other words, x/y = (xz)/(yz). This will help us because we can multiply the numerator (which consists of 1/4, 1/3, and –1/5) by 60, and then mutiply the denominator (which consists of 1/2, –1/6, and 1) by 60, thereby ridding us of fractions in the numerator and denominator. This process is shown below:

=  =

=

This means that a/b = 23/80. We are told that a and b are both positive and that their greatest common factor is 1. In other words, a/b must be the simplified form of 23/80. When a fraction is in simplest form, the greatest common factor of the numerator and denominator equals one. Since 23/80 is simplified, a = 23, and b = 80. The sum of a and b is thus 23 + 80 = 103.

The answer is 103.

To simply a fraction with variables, subtract exponents of like bases:

This leaves us with the expression:

Next, we know that to change negative exponents in the numerator into positive exponents, we place them in the denominator. Thus, our expression simplifies to:

The  and  variables with negative exponents can be rewritten with positive exponents by moving them from the denominator to the numerator, and vice versa. Therefore, the expression can be rewritten as

 .

The exponents on the denominator can then be subtracted from the exponent in the numerator to give

The expression can be rewritten as 

Now the expression can be combined by adding and subtracting exponents