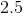Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Functions

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Functions

What is the domain of the following function?

$f(x)=\frac{1}{1+\cos(x)}$

Possible Answers:

$\mathbb{R}-\{\pi\}$

$\text{The set of all reals}$

- $\mathbb{R}-\{\pi ,3\pi\}$

$\mathbb{R}-\{-\pi\}$

$\mathbb{R}-\{{(2k+1)\pi\, ,$ k\in 0,1,2,3,4,.......\}$

Correct answer:

$\mathbb{R}-\{{(2k+1)\pi\, ,$ k\in 0,1,2,3,4,.......\}$

Explanation:

The denominator becomes zero whenever cos(x) becomes -1 and this happens when x is an odd multiple of $\pi$ . To avoid division by zero, we exclude all these numbers. Therefore the domain is:

$\mathbb{R}-\{{(2k+1)\pi\, ,$ k\in 0,1,2,3,4,.......\}$

Report an Error

Example Question #1 : Algebra Of Functions

Simplify the following expression:

x^4y^3z^2*x^2y^3z^4

Possible Answers:

$\frac{x^2}{z^2}$

$\frac{1}{x^6y^6z^6}$

$\frac{z^2}{x^2}$

x^2z^2

x^6y^6z^6

Correct answer:

x^6y^6z^6

Explanation:

When multiplying polynomials, add their exponents.

x:4+2=6

y:3+3=6

z:2+4=6

x^6y^6z^6

Report an Error

Example Question #2 : Algebra Of Functions

Simplify this polynomial:

$\frac{x^4y^3z^2}{x^2y^3z^4}$

Possible Answers:

x^6y^6z^6

$\frac{z^2}{x^2}$

$\frac{1}{x^6y^6z^6}$

$\frac{x^2}{z^2}$

Correct answer:

$\frac{x^2}{z^2}$

Explanation:

When dividing polynomials, you must subtract corresponding exponents.

x:4-2=2

y:3-3=0

z:2-4=-2

Thus, our answer is

$x^2y^0z^{-2}=\frac{x^2}{z^2}$ .

Report an Error

Example Question #3 : Algebra Of Functions

Simplify the following:

$\frac{x^4y^{-1}z^2}{x^{-3}y^2z^2}$

Possible Answers:

$\frac{x^7z^4}{y^2}$

$\frac{x}{y}$

$\frac{x}{y^3}$

$\frac{x^7}{y^3}$

Correct answer:

$\frac{x^7}{y^3}$

Explanation:

When dividing, we must subtract the exponents.

x:4-(-3)=7

y=-1-2=-3

z=2-2=0

Thus, our answer is $\frac{x^7}{y^3}$ .

Report an Error

Example Question #1 : Piecewise Functions

Let

$y=\left\{\begin{matrix} 2x&x\leq 0\\ x+9& x>0 \end{matrix}\right.$

What does equal when x=3 ?

Possible Answers:

Correct answer:

Explanation:

Because 3>0 we plug the x value into the bottom equation.

x=3

y=x+9

y=3+9=12

Report an Error

Example Question #1 : Piecewise Functions

Let

$y=\left\{\begin{matrix} x-9&x\leq 0\\ x+9& x>0 \end{matrix}\right.$

What does equal when x=0 ?

Possible Answers:

Correct answer:

Explanation:

Because $0\leq0$ we use the first equation.

y=x-9

Therefore, plugging in x=0 into the above equation we get the following,

y=0-9=-9 .

Report an Error

Example Question #1 : Piecewise Functions

Determine the value of f(1) if the function is

$f(x)=\left\{\begin{matrix} x& x<3\\ \pi&x=3 \\ 4&x>3 \end{matrix}\right.$

Possible Answers:

f(1)=1

f(1)=3

f(1)=4

$f(1)=\pi$

Correct answer:

f(1)=1

Explanation:

In order to determine the value of f(1) of the function we set x=1.

The value comes from the function in the first row of the piecewise function, and as such

f(1)=1

Report an Error

Example Question #1 : Piecewise Functions

Determine the value of f(1) if the function is

$f(x)=\left\{\begin{matrix} \sqrt{x}& 0\leq x<4\\ \3&x=4 \\ e^{-x}&x>4 \end{matrix}\right.$

Possible Answers:

$f(1)=\frac{1}{e}$

f(1)=3

f(1)=1

f(1)=3

Correct answer:

f(1)=1

Explanation:

In order to determine the value of f(1) of the function we set x=1.

The value comes from the function in the first row of the piecewise function, and as such

$f(1)=\sqrt{1}=1$

Report an Error

Example Question #1 : Piecewise Functions

For the function f(x) defined below, what is the value of f(x) when x=3 ?

$f(x)=\left\{\begin{matrix} -x+1&\text{ for }x<1\\ x^{2}-2&\text{ for }1< x< 3\\ 2^{x}&\text{ for }x\geq 3 \end{matrix}$

Possible Answers:

-2

Correct answer:

Explanation:

Evaluate the function for x=3 . Based on the domains of the three given expressions, you would use $2^{x}$ , since is greater than or equal to .

$2^{x}=2^{3}=8$

Report an Error

Example Question #1 : Greatest Integer Functions

If is the greatest integer function, what is the value of F(2.4) ?

Possible Answers:

2.5

Correct answer:

Explanation:

The greatest integer function takes an input and produces the greatest integer less than the input. Thus, the output is always smaller than the input and is an integer itself. Since our input was 2.4 , we are looking for an integer less than this, which must be since any smaller integer would by definition not be "greatest".

Report an Error

View Pre-Calculus Tutors

Joseph
Certified Tutor

Bank Street College of Education , Master's/Graduate, Early Childhood and Childhood General Education.

View Pre-Calculus Tutors

Nicholas
Certified Tutor

Salem State University, Bachelor of Science, GIS Technology.

View Pre-Calculus Tutors

Matthew
Certified Tutor

Bluffton University, Bachelor of Education, Mathematics. Bluffton University, Masters in Education, Education.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Philadelphia, SSAT Tutors in Washington DC, ISEE Tutors in Dallas Fort Worth, Calculus Tutors in Miami, Computer Science Tutors in New York City, ISEE Tutors in Atlanta, Biology Tutors in Philadelphia, Biology Tutors in Phoenix, Physics Tutors in Seattle, French Tutors in Dallas Fort Worth

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, ACT Courses & Classes in Seattle, GMAT Courses & Classes in Houston, Spanish Courses & Classes in Boston, GRE Courses & Classes in Chicago, LSAT Courses & Classes in Phoenix, ACT Courses & Classes in Atlanta, LSAT Courses & Classes in Denver, SAT Courses & Classes in Phoenix, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

SAT Test Prep in Los Angeles, ISEE Test Prep in Miami, ISEE Test Prep in Boston, GRE Test Prep in Seattle, MCAT Test Prep in Phoenix, MCAT Test Prep in Atlanta, GRE Test Prep in Chicago, MCAT Test Prep in Los Angeles, ACT Test Prep in Seattle, SSAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Functions

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #21 : Functions

Example Question #1 : Algebra Of Functions

Example Question #2 : Algebra Of Functions

Example Question #3 : Algebra Of Functions

Example Question #1 : Piecewise Functions

Example Question #1 : Piecewise Functions

Example Question #1 : Piecewise Functions

Example Question #1 : Piecewise Functions

Example Question #1 : Piecewise Functions

Example Question #1 : Greatest Integer Functions

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: