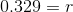Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Exponential and Logarithmic Functions

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Application Problems

Suppose you took out a loan years ago that gains $6.9\%$ interest. Suppose that you haven't made any payments on it yet, and right now you owe $\$100000$ on the loan. How much was the loan worth when you took it out?

Possible Answers:

$\$35789.47$

None of the other answers.

$\$38734.83$

$\$89558.26$

$\$51312.47$

Correct answer:

$\$51312.47$

Explanation:

The formula for the compund interest is as follows:

A = P(1+i)^t

By substuting known values into the compound interest formula, we have:

$100000 = P(1.069)^{10}$ .

From here, substitute known values.

$\frac{100000}{1.069^{10}} = P$

Divide by $1.069^{10}$

51312.47 = P

Report an Error

Example Question #1 : Application Problems

How many years does it take for $\$1000$ to grow into $\$5000$ when the $\$1000$ is deposited into a savings account that gains $3\%$ annual compound interest?

Possible Answers:

years

None of the other answers.

years

Correct answer:

None of the other answers.

Explanation:

The correct answer is about 54.45 years.

To find the number of years required, we solve the compound interest formula for .

The formula is as follows:

A = P(1+i)^t

Substitute known values.

5000 = 1000(1+.03)^t

Divide by 1000 .

5 = (1.03)^t

Take the natural log of both sides.

$\ln5 = \ln ((1.05)^t)$

Use the log power rule.

$\ln5 = t\ln1.03$

Divide by $\ln1.03$ .

$\frac{\ln5}{\ln1.03} = t$

54.44869 = t use a calculator to simplify.

Report an Error

Example Question #6 : Application Problems

The amount of phosphorus present in a sample at a given time is given by the following equation:

$Q(t)=Q_0e^{-0.03t}$

Where is in days, Q(t) is the amount of phosphorus after days, and Q_0 is the initial amount of phosphorus at the beginning of the first day. What percent of the initial amount of phosphorus is left after days of decay?

Possible Answers:

$83\%$

$11\%$

$23\%$

$47\%$

$56\%$

Correct answer:

$47\%$

Explanation:

The problem asks us for the percent that the amount of phosphorus after t days is of the original amount of phosphorus. If we think of this percentage with respect to the variables present in the equation, we can see that the following fraction expresses the amount of phosphorus after t days as a percentage of the initial amount of phosphorus:

$\frac{Q(t)}{Q_0}$

So if this is the fraction we want to solve for, we should divide both sides of the equation by Q_0 to obtain this fraction on the left side of the equation:

$Q(t)=Q_0e^{-0.03t}$

$\frac{Q(t)}{Q_0}=\frac{Q_0e^{-0.03t}}{Q_0}$

$\frac{Q(t)}{Q_0}=e^{-0.03t}$

We now have the fraction we want to solve for in terms of just one variable, , for which we plug in 25 days to find the percentage of phosphorus left of the initial amount after 25 days:

$\frac{Q(25)}{Q_0}=e^{-0.03(25)}=0.47$

So after 25 days of decay, the amount of phosphorus is 47% of the initial amount.

Report an Error

Example Question #2 : Application Problems

The exponential decay of an element is given by the following function:

$Q(t)=Q_0e^{-0.04223t}$

Where Q(t) is the amount of the element left after days, and Q_0 is the initial amount of the element. If there are kg of the element left after days, what was the initial amount of the element?

Possible Answers:

106.3 kg

127.1 kg

45.3 kg

63.7 kg

82.4 kg

Correct answer:

106.3 kg

Explanation:

The problem asks us for the initial amount of the element, so first let's solve our equation for Q_0 :

$Q(t)=Q_0e^{-0.04223t}$

$Q_0=Q(t)e^{0.04223t}$

The problem tells us that 25 days has passed, which gives us , and it also tells us the amount left after 25 days, which gives us Q(25) . Now that we have our equation for Q_0 , we can plug in the given values to find the initial amount of the element:

$Q_0=Q(25)e^{0.04223(25)}=(37)e^{0.04223(25)}=106.3$ kg

Report an Error

Example Question #3 : Application Problems

The exponential decay of an element is given by the function:

$Q(t) = Q_oe^{-0.42t}$

In this function, Q(t) is the amount of the element left after days, and Q_o is the initial amount of the element. If $25\:kg$ of the element is left after seven days, how much of the element was there to begin with, rounded to the nearest kilogram?

Possible Answers:

$180\:kg$

$473\:kg$

$512\:kg$

$122\:kg$

$140\:kg$

Correct answer:

$473\:kg$

Explanation:

To find the initial amount, you must rearrange the equation to solve for Q_o :

$Q(t) = Q_oe^{-0.42t}$

Divide both sides by $e^{-0.42t}$ :

$Q_o = \frac{Q(t)}{e^{-0.42t}}$

Substituting in the values from the problem gives

$Q_o = \frac{25}{e^{-0.42(7)}} \approx 473\:kg$

Report an Error

Example Question #8 : Application Problems

The exponential decay of an element is given by the function

$Q(t) = Q_o e^{-0.9t}$

In this function, Q(t) is the amount left after days, and Q_o is the initial amount of the element. What percent of the element is left after ten days, rounded to the nearest whole percent?

Possible Answers:

$10\%$

$52\%$

$0\%$

$47\%$

$26\%$

Correct answer:

$0\%$

Explanation:

To find the final percentage of the element left, we must rearrange the equation to solve for $e^{-0.9t}$ :

$\frac{Q(t)}{Q_o} = e^{-0.9t}$

Now, using the ten days as , we can solve for the percent of the element left after ten days:

$\frac{Q(10)}{Q_o} = e^{-0.9*10} \approx 0.0001 = 0.01\% \approx 0\%$

Report an Error

Example Question #11 : Application Problems

The exponential decay of an element is given by the function

$Q(t) = Q_o e^{-0.0327t}$

where Q(t) is the amount of the element after days, and Q_o is the initial amount of the element. If $3 \:kg$ of the element are left after four days, how much of the element was there initially, to the nearest tenth of a kilogram?

Possible Answers:

$2.9\:kg$

$3.4\:kg$

$3.3\:kg$

$3.1\:kg$

$3.2\:kg$

Correct answer:

$3.4\:kg$

Explanation:

To solve for the initial amount, we must use rearrange the equation:

$Q_o = \frac{Q(t)}{e^{-0.0327t}}$

We now substitute the values given from the problem

$Q_o = \frac{Q(4)}{e^{-0.0327*4}} = \frac{3}{e^{-0.0327*4}} = 3.4\:kg$

Report an Error

Example Question #12 : Application Problems

There were 240mg of caffeine in the discontinued energy drink. The decay rate for caffeine in the human bloodstream is around 0.14. If Jackie drinks this energy drink around 8PM, how much caffeine will still be in her system at midnight?

Possible Answers:

137.1 mg

29.2 mg

119.2mg

157.7mg

420.2 mg

Correct answer:

137.1 mg

Explanation:

Because this is a process taking place in the human body, we should use the exponential decay formula involving e:

$A=P*e^{rt}$

where A is the current amount, P is the initial amount, r is the rate of growth/decay, and t is time.

In this case, since the amount of caffeine is decreasing rather than increasing, use r=-0.14 . Between 8PM and midnight, 4 hours pass, so use t=4 . The initial amount of caffeine is given as 240 mg, so use P=240 .

Now evaluate:

$\\ A = 240\cdot e^{-0.14\cdot 4} \\ \\= 240\cdot e^{-0.56} \approx 240 \cdot 0.57 \\ \\= 137.1$

Report an Error

Example Question #1124 : Algebra

Stuff animals were a strange craze of the 90's. A Cat stuff animal with white paws sold for $6 in 1997. In 2015, the Cat will sell for $1015. What has been the approximate rate of growth for these stuff animal felines?

Possible Answers:

$33 \%$

$16.8 \%$

$13.29 \%$

$3.2 \%$

$168 \%$

Correct answer:

$33 \%$

Explanation:

Use the formula for exponential growth y = A*(1+r)^t where y is the current value, A is the initial value, r is the rate of growth, and t is time. Between 1997 and 2015, 18 years passed, so use t=18 . The stuffed animal was originally worth $6, so A=6 . It is now worth $1,015, so y=1015 .

Our equation is now:

$1015 = 6*(1+r)^{18}$ divide by 6:

$169.1\overline{6}=(1+r)^{18}$ take both sides to the power of $\frac{1}{18}=0.0\overline{5}$ :

$1.329 \approx 1+r$ subtract 1

0.329 = r

As a percent, r is about 33%.

Report an Error

View Pre-Calculus Tutors

Travis
Certified Tutor

Delaware State University, Bachelor of Science, Mathematics.

View Pre-Calculus Tutors

Dossevi
Certified Tutor

cole Ste Genevive Versailles, Bachelor of Science, Mathematics. Institut National Polytechnique de Grenoble, Master of Scienc...

View Pre-Calculus Tutors

Alejandro
Certified Tutor

Kennesaw State University, Bachelor of Science, Computer Software Engineering.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in New York City, English Tutors in Boston, LSAT Tutors in Boston, English Tutors in New York City, Spanish Tutors in Atlanta, Spanish Tutors in Seattle, MCAT Tutors in Washington DC, Math Tutors in San Diego, English Tutors in San Francisco-Bay Area, Spanish Tutors in Boston

Popular Courses & Classes

LSAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Seattle, LSAT Courses & Classes in San Diego, Spanish Courses & Classes in Chicago, GRE Courses & Classes in Washington DC, Spanish Courses & Classes in New York City, SSAT Courses & Classes in Houston, GRE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

GRE Test Prep in Washington DC, ISEE Test Prep in Boston, SAT Test Prep in Atlanta, GMAT Test Prep in Denver, SAT Test Prep in Denver, SSAT Test Prep in Houston, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in New York City, GMAT Test Prep in Los Angeles, LSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Exponential and Logarithmic Functions

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #2 : Application Problems

Example Question #1 : Application Problems

Example Question #6 : Application Problems

Example Question #2 : Application Problems

Example Question #3 : Application Problems

Example Question #8 : Application Problems

Example Question #11 : Application Problems

Example Question #12 : Application Problems

Example Question #1124 : Algebra

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: