New SAT Writing and Language : New SAT
Study concepts, example questions & explanations for New SAT Writing and Language
All New SAT Writing and Language Resources
Example Questions
Example Question #2 : How To Multiply Integers
Janet can pick between 10 and 20 tomatoes in an hour. What is a possible amount of time for Janet to pick 120 tomatoes?
Since Janet can pick between 10 and 20 tomatoes in an hour, there is a range for which she can pick 120 tomatoes. Therefore, to find the possible amount of time it will take Janet to pick 120 tomatoes set up two fractions.
The first fraction will use the rate of 10 tomatoes an hour.
Therefore, identifying the variables are as follows.
Substituting these into the fraction results in a possible time
The second fraction will use the rate of 20 tomatoes an hour.
Therefore, identifying the variables are as follows.
Substituting these into the fraction results in a possible time
Of the answer selections 6 hours would be the correct answer.
Example Question #31 : New Sat Math Calculator
Jamie is three times her little brother's age, and her little brother is two years younger than his older brother. Collectively, the three of them are 27 years old. How old is Jamie?
None of the available answers
The algebraic expression for 
Jamie's youngest brother is five, the next oldest brother is seven, and Jamie is 15.
Example Question #2 : How To Graph A Point
Given the graph of record sales, what fraction of records were sold in 2004 to 2010?
Given the graph of record sales, to find the fraction of records that were sold in 2004 to 2010 first identify the record sales in 2004 and the record sales in 2010.
Examining the graph,
Record sales in 2004:14 million
Record sales in 2010: 13 million
From here, to find the fraction of records sold during this time period, use the following formula.
Example Question #2511 : Sat Mathematics
Fred has $100 in quarters and nickels. He initially has 260 quarters. He then exchanges some of his nickels for the dimes of a friend. He is left with a total of 650 coins (consisting of quarters, dimes and nickels) still worth $100. How many nickels does Fred have now?
Fred has $100 in quarters and nickels initially. We are also told that he has 260 quarters. This is worth $65. Thus Fred initially has $35 in nickels or 700 nickels.
Fred now exchanges some of his nickels for the dimes of a friend. He ends up with 650 coins. We know that Fred started with 960 coins (700 nickels + 260 quarters). He ends up with 650 coins. The number of quarters remains unchanged, meaning he now has 390 nickels and dimes. These must have the same value as the initial 700 nickels, though, since he didn't lose any money.
Now we can finally set up our solution:
Thus Fred has 80 nickels and 310 dimes.
An alternative solution step is to notice that turning nickels into dimes always occurs in exactly one way: 2 nickels to 1 dime. Every time you do this conversion, you will lose exactly one coin. We then notice that the number of coins drops from 960 to 650, or drops by 310 coins. We thus need to get rid of 310 coins. Since we're only allowed to change nickels into dimes (and lose 1 coin each time), we simply do this 310 times to reach the requisite number of coin losses. We are left with the proper number of coins with the proper value immediately. Since every replacement replaced 2 nickels, we also lost 
Example Question #41 : Cylinders
The figure below represents a cylinder with a smaller cylinder removed from its middle.
Find the volume of the figure.
In order to find the volume of the figure, we will first need to find the volume of both cylinders.
Recall how to find the volume of the cylinder:
Now, use the given radius and height to find the volume of the larger cylinder.
Next, use the given radius and height to find the volume of the smaller cylinder.
Subtract the volume of the smaller cylinder from the volume of the larger one to find the volume of the figure.
Make sure to round to 
Example Question #1 : How To Add Rational Expressions With A Common Denominator
Simplify the following rational expression:
Since both fractions in the expression have a common denominator of 
Example Question #3 : How To Find Simple Interest
If a student borrows $200,000 at an interest rate of 6% compounded annually, when she graduates in 4 years how much money will she owe? Round to the nearest dollar.
This problem requires knowledge of the compound interest formula,
Where 
We know that the student borrowed $200,000 compounded annually at a 6% interest rate, therefore by plugging in those numbers we find that after she graduates in 4 years she will owe $252,495.
Example Question #4 : How To Find Simple Interest
If a student borrows $200,000 at an interest rate of 6% compounded quarterly, when she graduates in 4 years how much money will she owe? Round to the nearest dollar.
This problem requires knowledge of the compound interest formula,
Where
We know that the student borrowed $200,000 compounded quarterly at a 6% interest rate, therefore by plugging in those numbers we find what she will owe after she graduates in 4 years.
Example Question #12 : Quadrilaterals
A square 
The area of 
Example Question #1 : Hexagons
Archimedes High School has an unusual track in that it is shaped like a regular hexagon, as above. Each side of the hexagon measures 264 feet.
Alvin runs at a steady speed of seven miles an hour for twelve minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?
Point E
Point D
Point B
Point F
Point C
Point E
Alvin runs at a rate of seven miles an hour for twelve minutes, or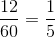 
One mile comprises 5,280 feet, so this is equal to
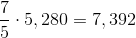
Since each side of the track measures 264 feet, this means that Alvin runs
which means that Alvin runs around the track four complete times, plus four more sides of the track. Alvin stops when he is at Point E.
All New SAT Writing and Language Resources
