All New SAT Writing and Language Resources
Example Questions
Example Question #3 : How To Graph A Quadratic Function
How many times does the equation below cross the x-axis?
You can solve this problem two ways.
3. You can solve for where the graph crosses the x-axis by setting the equation equal to zero, factoring, and solving.
2. You can quickly sketch the graph by choosing some x values and solving for y.


We see that the graph passes the x-axis twice.
Example Question #2 : How To Divide Complex Numbers
Simplify the expression by rationalizing the denominator, and write the result in standard form:
Multiply both numerator and denominator by the complex conjugate of the denominator, which is 
Example Question #232 : New Sat
Find the solutions for
The first step is to set it equal to zero.
Now we will use the quadratic formula.
In this case 

Example Question #141 : Sat Mathematics


The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 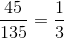
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

Example Question #371 : Geometry

If 


AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a 

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to 
which also means
Example Question #231 : New Sat
Find the solutions to
First step is to set it equal to zero
Now factor out an
Set up the equations, and solve for 
Example Question #81 : Systems Of Equations
Find the value of 
Subtracting the second equation from the first, we acquire 
Adding this equation to the third equation, we get 
Therefore, 
Example Question #232 : New Sat
The temperature at the surface of the ocean is 



This may seem confusing, but is pretty straightforward.
Thus, for every 125 meters below the surface, the temperature decreases by one degree.
To find how much it decreases with every 100 meters, we need to do the following:
Thus, the temperature decreases by 
Example Question #52 : New Sat Math No Calculator
Let 



None of these
The problem tells us that increasing 


Let's find an expression for increasing 
Let's find an expression for decreasing the product of four and 



Now we must set the two expressions equal to one another.
Subtract 


Now we can add five to both sides.
Now we can multiply both sides by 
The answer is:
Example Question #233 : New Sat
Solve the following system of equations:
What is the sum of 

This problem can be solved by using substitution. Write the first equation in terms of 
So 



So the sum of 

Certified Tutor
All New SAT Writing and Language Resources