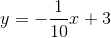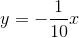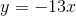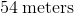We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

New SAT Writing and Language : New SAT

Study concepts, example questions & explanations for New SAT Writing and Language

Create An Account

All New SAT Writing and Language Resources

3 Diagnostic Tests 39 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : How To Find Compound Interest

A truck was bought for $\$ 20,000$ in 2008, and it depreciates at a rate of $13\%$ per year. What is the value of the truck in 2016? Round to the nearest cent.

Possible Answers:

y= 6664.23

y= 5664.23

y= 6564.23

y= 16564

y= 6764.23

Correct answer:

y= 6564.23

Explanation:

The first step is to convert the depreciation rate into a decimal. $13\%=0.13$ . Now lets recall the exponential decay model. y=C(1-r)^t , where is the starting amount of money, is the annual rate of decay, and is time (in years). After substituting, we get

y=20000(1-0.13)^8

y=20000(0.87)^8

$y=20000\cdot 0.3282117$

y= 6564.23

Report an Error

Example Question #191 : New Sat

What is $320^{\circ}$ in radians?

Possible Answers:

$\frac{9\pi}{16}$

$\frac{\pi}{9}$

$-\frac{13\pi}{9}$

$\frac{16}{9}$

$\frac{16\pi}{9}$

Correct answer:

$\frac{16\pi}{9}$

Explanation:

To convert degrees to radians, we need to remember the following formula.

$\mbox{degrees}\cdot \frac{\pi}{180}$ .

Now lets substitute for degrees.

$320\cdot \frac{\pi}{180}=\frac{16\pi}{9}$

Report an Error

Example Question #81 : Coordinate Geometry

Trans

Lines P and Q are parallel. Find the value of .

Possible Answers:

$x= \sqrt{ 205}$

$x=-5+ \sqrt{ 205}$

$x=-5- \sqrt{ 205}$

$x=\pm \sqrt{ 205}$

$x=5 + \sqrt{ 205}$

Correct answer:

$x=-5+ \sqrt{ 205}$

Explanation:

Since these are complementary angles, we can set up the following equation.

x^2+4+10x-4=180

x^2+10x=180

x^2+10x-180=0

Now we will use the quadratic formula to solve for .

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

$x=\frac{-10\pm \sqrt{10^2-4(1)(-180)}}{2(1)}$

$x=\frac{-10\pm \sqrt{100+720}}{2}$

$x=\frac{-10\pm \sqrt{820}}{2}$

$x=\frac{-10\pm \sqrt{4\cdot 205}}{2}$

$x=\frac{-10\pm 2\sqrt{ 205}}{2}$

$x=-5\pm \sqrt{ 205}$

Note, however, that the measure of an angle cannot be negative, so $x=-5- \sqrt{ 205}$ is not a viable answer. The correct answer, then, is $x=-5+ \sqrt{ 205}$

Report an Error

Example Question #192 : New Sat

Find the equation of a line that goes through the points (0,3) , and (-10,4) .

Possible Answers:

$y=-\frac{1}{10}x+3$

y=-13x

y=-10x

y=-10x+3

$y=-\frac{1}{10}x$

Correct answer:

$y=-\frac{1}{10}x+3$

Explanation:

For finding the equation of a line, we will be using point-slope form, which is

y-y_0=m(x-x_0) , where is the slope, and (x_0, y_0) is a point.

$m=\frac{y_2-y_1}{x_2-x_1}=\frac{4-3}{-10-0}=\frac{1}{-10}=-\frac{1}{10}$

We will pick the point (0,3)

$y-3=-\frac{1}{10}(x-0)$

$y=-\frac{1}{10}x+3$

If we picked the point (-10,4)

$y-4=-\frac{1}{10}(x+10)$

$y=-\frac{1}{10}x-1+4$

$y=-\frac{1}{10}x+3$

We get the same result

Report an Error

Example Question #193 : New Sat

Find the equation of a line that passes through the point (-2,5) , and is parallel to the line y=-3x+4 .

Possible Answers:

y=-3x+1

y=-3x

y=-3x-3

y=-3x-1

y=-3x-10

Correct answer:

y=-3x-1

Explanation:

Since we want a line that is parallel, we will have the same slope as the line (-3) . We can use point slope form to create an equation.

y-y_0=m(x-x_0) , where is the slope and (x_0, y_0) is a point.

y-5=-3(x-(-2))

y-5=-3(x+2)

y-5=-3x-6

y=-3x-1

Report an Error

Example Question #1 : How To Find The Perimeter Of A Rectangle

A rectangular garden has an area of $80\: \mbox{m^2}$ . Its length is meters longer than its width. How much fencing is needed to enclose the garden?

Possible Answers:

$36\: \mbox{meters}$

$54\: \mbox{meters}$

$18\: \mbox{meters}$

$40\: \mbox{meters}$

$24\: \mbox{meters}$

Correct answer:

$36\: \mbox{meters}$

Explanation:

We define the variables as $w = \mbox{width}$ and $l = \mbox{length} = w + 2$ .

We substitute these values into the equation for the area of a rectangle and get $A_{\mbox{rectangle} }= wl = w(w + 2) = 80$ .

w^2 +2w-80=0

(w - 8)(w + 10) = 0

w = 8 or w = -10

Lengths cannot be negative, so the only correct answer is w = 8 . If w = 8 , then l = 10 .

Therefore, $\mbox{perimeter }= 2w + 2l = 16 + 20 = 36\:\mbox{m}$ .

Report an Error

Example Question #15 : New Sat Math No Calculator

If 3x + 72 = 9x + 120 , what does equal?

Possible Answers:

Correct answer:

Explanation:

Subtract and from the both sides to get -6x = 48 .

Divide both sides by , to get

$x=\frac{48}{-6}=-8$

Report an Error

Example Question #3 : How To Graph A Quadratic Function

Screen shot 2016 02 10 at 1.10.30 pm

What is the equation of the graph?

Possible Answers:

y=x^2-4x-4

y=ax^2-4x+4

y=2x^2-4x-4

y=2x^2 +4x+4

y=2x^2-4x+4

Correct answer:

y=2x^2-4x+4

Explanation:

In order to figure out what the equation of the image is, we need to find the vertex. From the graph we can determine that the vertex is at (1,2) . We can use vertex form to solve for the equation of this graph.

Recall vertex form,

y=a(x-h)^2+k , where is the coordinate of the vertex, and is the coordinate of the vertex.

Plugging in our values, we get

y=a(x-1)^2+2

To solve for , we need to pick a point on the graph and plug it into our equation.

I will pick (-1,10) .

10=a(-1-1)^2+2

10=a(-2)^2+2

10=4a+2

8=4a

$a=\frac{8}{4}=2$

Now our equation is

y=2(x-1)^2+2

Let's expand this,

y=2(x^2-2x+1)+2

y=2x^2-4x+2+2

y=2x^2-4x+4

Report an Error

Example Question #194 : New Sat

Which expression is equivalent to the following quotient? For b>0, c>0 .

$\frac{10a^2b^{-3}c^3}{5bc^2}$

Possible Answers:

$\frac{2a^{-2}c}{b^4}$

$\frac{2a^2c}{b^4}$

$\frac{2ac}{b^2}$

$\frac{2a^2c}{b^{-4}}$

$\frac{2a^2c^0}{b^4}$

Correct answer:

$\frac{2a^2c}{b^4}$

Explanation:

All we need to do is remember the quotient rule for exponents.

$\frac{a^n}{a^m}=a^{n-m}$

We apply this to each term and we get the following.

$\frac{10a^2b^{-3}c^3}{5bc^2}=2a^2b^{-3-1}c^{3-2}=2a^2b^{-4}c^1=\frac{2a^2c}{b^4}$

Report an Error

Example Question #2 : How To Find The Solution To A Rational Equation With Lcd

Solve for x:

$\frac{x+3}{7}=3$

Possible Answers:

x=0

x=42

x=18

x=6

x=24

Correct answer:

x=18

Explanation:

The first step is to cancel out the denominator by multiplying both sides by 7:

$7\cdot \frac{x+3}{7}=3\cdot7$

x+3=21

Subtract 3 from both sides to get by itself:

x+3-3=21-3

x=18

Report an Error

View Tutors

Chernyeh
Certified Tutor

Purdue University-Main Campus, Bachelor of Science, Business Administration and Management.

View Tutors

Shifrah
Certified Tutor

University of Maryland-Baltimore County, Bachelor of Science, Biology, General. Massachusetts College of Pharmacy and Health ...

View Tutors

Rodney
Certified Tutor

University of Washington, Master's/Graduate, Economics.

All New SAT Writing and Language Resources

3 Diagnostic Tests 39 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Denver, Physics Tutors in Denver, MCAT Tutors in Chicago, SAT Tutors in Chicago, Reading Tutors in Denver, MCAT Tutors in Los Angeles, Math Tutors in Phoenix, French Tutors in Seattle, Chemistry Tutors in New York City, Physics Tutors in Phoenix

Popular Courses & Classes

Spanish Courses & Classes in Miami, ISEE Courses & Classes in Los Angeles, Spanish Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in Atlanta, MCAT Courses & Classes in Miami, MCAT Courses & Classes in New York City, ISEE Courses & Classes in Seattle, SSAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Denver, SSAT Test Prep in Phoenix, GMAT Test Prep in Houston, ACT Test Prep in Phoenix, GMAT Test Prep in Boston, SSAT Test Prep in Boston, LSAT Test Prep in Atlanta, ISEE Test Prep in Chicago, SSAT Test Prep in Los Angeles, ISEE Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

New SAT Writing and Language : New SAT

Study concepts, example questions & explanations for New SAT Writing and Language

All New SAT Writing and Language Resources

Example Questions

Example Question #4 : How To Find Compound Interest

Example Question #191 : New Sat

Example Question #81 : Coordinate Geometry

Example Question #192 : New Sat

Example Question #193 : New Sat

Example Question #1 : How To Find The Perimeter Of A Rectangle

Example Question #15 : New Sat Math No Calculator

Example Question #3 : How To Graph A Quadratic Function

Example Question #194 : New Sat

Example Question #2 : How To Find The Solution To A Rational Equation With Lcd

All New SAT Writing and Language Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: