You can solve this problem two ways. 

3. You can solve for where the graph crosses the x-axis by setting the equation equal to zero, factoring, and solving. 

2. You can quickly sketch the graph by choosing some x values and solving for y.

We see that the graph passes the x-axis twice. 

Multiply both numerator and denominator by the complex conjugate of the denominator, which is :

The first step is to set it equal to zero.

Now we will use the quadratic formula.

In this case , , 

The perimeter is equal to the sum of the three sides.  In similar triangles, each side is in proportion to its correlating side.  The perimeters are also in equal proportion.

Perimeter A = 45” and perimeter B = 135”

The proportion of Perimeter A to Perimeter B is .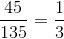 

This applies to the sides of the triangle.  Therefore to get the any side of Triangle B, just multiply the correlating side by 3.

15” x 3 = 45”

10” x 3 = 30“

AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.

Since we have a  triangle, the opposites sides of those angles will be in the ratio .

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to .

which also means

First step is to set it equal to zero

Now factor out an 

Set up the equations, and solve for .

Subtracting the second equation from the first, we acquire .

Adding this equation to the third equation, we get .

Therefore, .

This may seem confusing, but is pretty straightforward.

Thus, for every 125 meters below the surface, the temperature decreases by one degree.

To find how much it decreases with every 100 meters, we need to do the following:

Thus, the temperature decreases by  every 100 meters.

The problem tells us that increasing  by twenty percent gives us the same thing that we would get if we decreased the product of four and  by five. We need to find expressions for these two situations, and then we can set them equal and solve for .

Let's find an expression for increasing  by twenty percent. We could represent this as the following:

Let's find an expression for decreasing the product of four and  by five. First, we must find the product of four and , which can be written as . Then we must decrease this by five, so we must subtract five from , which could be written as the following:

Now we must set the two expressions equal to one another.

Subtract  from both sides. We can rewrite  as  so that it has a common denominator with  

Now we can add five to both sides.

Now we can multiply both sides by , which is the reciprocal of 

The answer is:

This problem can be solved by using substitution.  Write the first equation  in terms of  and substitute it into the second equation.

So  and thus  and solving for  and then .

So the sum of  and  is 7.