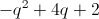The complex conjugate of a complex number  is , so  has  as its complex conjugate. The sum of the two numbers is

Write the following sentence by parts.

A number squared:  

The difference of six and a number squared:  

Is four:  

Combine the parts to write an equation.

The answer is:  

To solve this problem, first recall the equation of a line.

where

Remember that slope is the rate of change that occurs in a function and that the -intercept is the  value corresponding to an  value equalling zero.

Now, identify what is known.

"Billy buys a tomato plant that is 4 inches tall. With regular watering the plant grows 3 inches a year."

Since the height of Billy's plant is 4 inches tall when he gets it, at time being zero. It is also stated that the plant grows 3 inches per year, this is the rate of change of the plant's height. Writing the known information in mathematical terms results as follows.

In this case our 

Therefore, the -intercept represents the starting height of the plant which is 4 inches.

To solve this problem, first recall the equation of a line.

where

Remember that slope is the rate of change that occurs in a function and that the -intercept is the  value corresponding to an  value equalling zero.

Now, identify what is known.

"Billy buys a tomato plant that is 4 inches tall. With regular watering the plant grows 3 inches a year."

Since the height of Billy's plant is 4 inches tall when he gets it, at time being zero. It is also stated that the plant grows 3 inches per year, this is the rate of change of the plant's height. Writing the known information in mathematical terms results as follows.

In this case our 

Therefore, the slope represents the rate of change in the height of the plant which is 3 inches per year.

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.

Add like terms together:

has no like terms.

Combine these terms into one expression to find the answer:

To solve for , simplify the fraction. In order to do this, recall that dividing by a fraction is the same as multiplying by its reciprocal. Therefore, rewrite the equation as follows.

Now, simplify the first fraction by calculating four squared.

From here, factor the denominator of the second fraction.

Next, factor the 16.

From here, cancel out like terms that are in both the numerator and denominator. In this particular case that includes (x-2) and 2.

Now, distribute the eight.

Next, multiply both sides by the denominator.

The (8x+16) cancels out and leaves the following equation.

Now to solve for  perform opposite operations to move all numerical values to one side of the equation leaving  by itself on the other side of the equation.

To solve this problem first manipulate the given equation to solve for .

Multiply by  on both sides. The 's on the left hand side of the equation will cancel out.

Now to calculate , substitute the value for  that was just found, into the denominator and simplify by canceling out common factors.

We can solve either by substitution or by elimination. We will solve by elimination.

Line up both equations so the variables are in the same order.

Because we have a negative  and a positive , if we were to add these two equations straight up and down, the  values would cancel out.

Solve for .

Plug  back in to one of the original equations to solve for .

The final answer will be . We can check this answer by plugging it back into either of the original equations.

This question is testing the knowledge and skills of calculating a function value. Similar to domain and range, calculating the function value requires the application of input values into the function to find the output value. In other words, evaluating a function at a particular value results in the function value; which is another way of saying function value is the output. 

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Identify the input value.

Since the function is in the form  and the question asks to calculate  we know that the input value is six.

Step 2: Given the function, input the desired  value. 

In step one the input value of six was found. Now substitute 6 in for every in the function.

Step 3: Verify solution by graphing the function.

To find the function value on a graph go to  and find the y value that lies on the graph at . Looking at the graph above when , .

Recall that , thus verifying the solution found in step 2.

Let x be the number of pencils and y be the number of pens Sally purchased. We are told that each pencil costs 25 cents. Because, the total amount she spent was given in dollars, we want to convert 25 cents to dollars. Because there are 100 cents in one dollar, 25 cents  = $0.25. Similarly, each pen costs $0.50.

The amount that Sally spent on pencils is equal to the product of the number of pencils and the cost per pencil. We can model the amount of money spent on pencils as 0.25x.

Likewise, the amount Sally spent on pens is equal to the product of the number of pens and the cost per pen, or 0.5y.

Since we are told that Sally spent $5.75 total on pens and pencils combined, we can write the following:

We are also told that the number of pens is one greater than the number of pencils. We can thus write:

We now have two equations and two unknowns. In order to solve this system of equations, we can take the value of y = x + 1 and substitute it into the other equation.

Distribute.

Combine x terms.

Subtract 0.5 from both sides.

Divide both sides by 0.75.

This means Sally bought 7 pencils and 8 pens. The question asks us to find the number of pens and pencils purchased altogether, which would equal

The answer is 15.