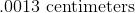All New SAT Math - Calculator Resources
Example Questions
Example Question #472 : New Sat
A blue train leaves San Francisco at 8AM going 80 miles per hour. At the same time, a green train leaves Los Angeles, 380 miles away, going 60 miles per hour. Assuming that they are headed towards each other, when will they meet, and about how far away will they be from San Francisco?
The two trains will never meet.
Around 10:43AM, about 217.12 miles away from San Francisco
Around 3AM the next day, about 1,520 miles away from San Francisco
Around 2:45AM, about 200.15 miles away from San Francisco
Around 10:43AM, about 217.12 miles away from San Francisco
This system can be solved a variety of ways, including graphing. To solve algebraically, write an equation for each of the different trains. We will use y to represent the distance from San Francisco, and x to represent the time since 8AM.
The blue train travels 80 miles per hour, so it adds 80 to the distance from San Francisco every hour. Algebraically, this can be written as 
The green train starts 380 miles away from San Francisco and subtracts distance every hour. This equation should be 
To figure out where these trains' paths will intersect, we can set both right sides equal to each other, since the left side of each is 



Since we wrote the equation meaning time for 

To figure out how far from San Francisco they are, figure out how many miles the blue train could have gone in 2.714 hours. In other words, plug 2.714 back into the equation 

Example Question #32 : Convert Among Different Sized Standard Measurement Units: Ccss.Math.Content.5.Md.A.1
How many 
To solve this problem we can make proportions.
We know that 
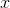
Next, we want to cross multiply and divide to isolate the on one side.
The 
Example Question #472 : New Sat
How many 
To solve this problem we can make proportions.
We know that 

Next, we want to cross multiply and divide to isolate the on one side.
The 
Example Question #93 : Numbers And Operations
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #533 : Arithmetic
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #534 : Arithmetic
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #1 : Solving Word Problems With One Unit Conversions
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #541 : Arithmetic
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 


Example Question #72 : Ratios & Proportional Relationships
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
Reduce.
The carpenter needs 
Example Question #72 : Ratios & Proportional Relationships
A carpenter is making a model house and he buys 

We can solve this problem using ratios. There are 

We know that the carpenter needs 

Now, we can solve for 
Cross multiply and solve for 
Simplify.
Divide both sides by 
Solve.
The carpenter needs 
All New SAT Math - Calculator Resources