MCAT Physical : Work, Energy, and Power
Study concepts, example questions & explanations for MCAT Physical
All MCAT Physical Resources
Example Questions
Example Question #1 : Potential Energy (Gravitational And Spring)
A block with mass, 
The spring potential is given by the equation 
When 
Example Question #1 : Potential Energy (Gravitational And Spring)
A certain chocolate candy bar contains 
Our first step is to convert kilocalories to Joules.
Now that we have converted to standard units, we can use the formula for gravitational potential energy to find the height.
We know our energy limit from the candy bar, the mass of the barbell, and the gravitational acceleration.
Solve to isolate the height.
Note that we end up with kilometers because we used kilojoules in our calculation.
Example Question #2 : Potential Energy (Gravitational And Spring)
A 2kg mass is suspended on a rope that wraps around a frictionless pulley attached to the ceiling with a mass of 0.01kg and a radius of 0.25m. The other end of the rope is attached to a massless suspended platform, upon which 0.5kg weights may be placed. While the system is initially at equilibrium, the rope is later cut above the weight, and the platform subsequently raised by pulling on the rope.
After the rope is cut and the platform falls, we want to pull the platform back up to 5m above the ground. How much energy is required to raise the platform?
75J
50J
200J
98J
98J
First, we need to understand what type of energy we are considering. As the resistive force to motion is due to gravity, we are talking about gravitational potential energy. We need to use the formula U = mgh.
Plugging in the values that are provided, we can solve for the potential energy (U).
U = (2kg)(9.8m/s2)(5m) = 98J
The amount of work required is equal to the change in potential energy of the platform.
Example Question #1 : Potential Energy (Gravitational And Spring)
Two students (student X and student Y) lift a boulder vertically from point A to point B. Student X directly lifts the boulder from point A to point B, whereas student Y uses a pulley to lift the boulder. This allows student Y to apply a force (
The vertical distance between point A and point B is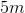 
Student Z uses an inclined plane to lift the boulder and exerts only one third of 
I. The change in potential energy
II. The distance travelled
III. The sum of the change in kinetic energy and change in potential energy
I only
II only
I and II
I and III
II only
The change in potential energy is defined as:
This means that the potential energy is only dependent on the change in vertical height, which is the same for both students. Since both students travel the same distance, the change in potential energy is equal and statement I is true.
Student X directly lift the boulder whereas student Z uses an inclined plane. Student Z slides the boulder along a larger distance than student X, even if their total displacement ends up begin equal; therefore, statement II is false.
Recall that the sum of change in kinetic energy and change in potential energy is equal to work, which is the same for both students (work is path independent in a gravitational field). The total work for both students will be equal, and statement III will be true.
The only statement that is not equal for both students is statement II.
Example Question #1 : Potential Energy (Gravitational And Spring)
A 2kg lead ball is loaded into a spring cannon and the cannon is set at a 45º angle on a platform. The spring has a spring constant of 100N/m and the ball and spring system is compressed by 1m before launch. While the ball is in flight air resistance can be neglected, and the ball finishes its flight by landing at a cushion placed some distance away from the cannon.
How much energy is stored in the spring before the ball is launched?
20J
20kJ
50J
50kJ
50J
In order to determine how much energy is stored, we first need to understand what type of energy we want to consider. A spring stores potential energy; the potential energy of the spring is maximized at maximal displacement from its resting state. In order to compute the potential energy stored, we need both the spring constant (100N/m) and the displacement from resting (1m).
PEs = ½k(Δx)2 = ½(100N/m)(1m)2 = 50J
Example Question #1 : Potential Energy (Gravitational And Spring)
Two children are playing with sleds on a snow-covered hill. Sam weighs 50kg, and his sled weighs 10kg. Sally weighs 40kg, and her sled weighs 12kg. When they arrive, they climb up the hill using boots. Halfway up the 50-meter hill, Sally slips and rolls back down to the bottom. Sam continues climbing, and eventually Sally joins him at the top.
They then decide to sled down the hill, but disagree about who will go first.
Scenario 1:
Sam goes down the hill first, claiming that he will reach a higher velocity. If Sally had gone first, Sam says they could collide.
Scenario 2:
Sally goes down the hill first, claiming that she will experience lower friction and thus reach a higher velocity. If Sam had gone first, Sally says they could collide.
Scenario 3:
Unable to agree, Sam and Sally tether themselves with a rope and go down together.
How much potential energy does Sally have at the top of the hill on her sled?
260J
26kJ
2.6kJ
26,000kJ
260000J
26kJ
This is a tricky question only because you have to keep your units straight. The formula is simply PE = mgh.
PE = 52kg * 10m/s2 * 50m = 26,000J = 26kJ
Example Question #51 : Newtonian Mechanics And Motion
A 2kg box slides down a ramp a distance of two meters before it reaches the ground. The ramp has an angle of 30o. The coefficient of kinetic friction for the ramp is 0.1.
What is the gravitational potential energy of the box relative to the ground when at the top of the ramp?
Gravitational potential energy is determined using the equation 
Now that we have the height, we simply plug the given values into the equation.
Example Question #11 : Potential Energy (Gravitational And Spring)
A spring is used to launch a 
What was the displacement of the spring required to launch the ball?
We can use conservation of energy to calculate the displacement. The spring must be displaced so that its potential energy is equal to the gravitational potential energy of the ball at its maximum height.
Substituting in the expressions for potential energy of the spring and gravitational potential energy, we can start to set up an equation using the given variables.
We are given the spring constant, the mass, and the maximum height. Using these values, and the acceleration for gravity, we can solve for the spring displacement.
Note that, since we are taking the square root, the displacement answer could be either positive or negative. Since the spring is being compressed to launch the ball (rather than stretched), the displacement should be negative.
Example Question #31 : Work, Energy, And Power
What is the potential energy of a 
Our formula for gravitational potential energy is:
Example Question #12 : Potential Energy (Gravitational And Spring)
A 
It depends if the stone is raised vertically or along an incline
No matter how you raise the stone (all at once, in multiple vertical steps, or along a ramp) the final potential energy is the same. Gravitational potential energy of a given object is solely dependent on height.
Use the given mass, the acceleration of gravity, and the final height to calculate the potential energy of the system.
Since work is equal to the change in potential energy of a system, this value also gives the total work done to raise the stone.
Certified Tutor
Certified Tutor
All MCAT Physical Resources
