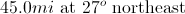This question requires us to find the end position relative to the starting position. As a result, 150m is not the correct answer; this would be the distance, not the displacement.

The first portion involves writing down that the person moves north 100m. At this point in time, his distance on the y-axis is +100m. Next, we have to see how the person's x-axis and y-axis distances change after turning left 120^o, and walking 50m.

For the x-axis, we use the equation based on a right triangle. By turning 120^o, the man is walking at an angle of 30^o to the x-axis. Since this is the only movement in the x-axis, the total distance on the x-axis is –43.3m (movement to the left will be negative).

For the y-axis, we use the equation Since this 25m is heading downward, we subtract it from the initial upward movement of 100m. As a result, the total movement in the y-axis is 75m.

Now that we have the component vectors, we can use the pythagorean theorem to determine the total displacement of the man.

A very quick and easy way to determine the total displacement of an object is to graph the velocity of the object over time, and calculate the area under the line. The velocity vs. time graph would show a triangle with a height of  and a base of 15 seconds. The area of a triangle is determined by the equation .

As a result, we conclude that the sprinter has a total displacement of 75m.

At maximum height, the projectile is still moving in the x-direction. The horizontal component of velocity remains constant during projectile motion, therefore  .

Gravity is always acting on any body in projectile motion, therefore  . Acceleration will be constant at .

Inconstant velocity implies a non-zero acceleration. A non-zero acceleration implies a non-zero force.

Circular motion is made possible by acceleration along the radius of the circle. Since there is acceleration, the linear velocity is not constant even if angular velocity is constant.

The other scenarios describe instances in which there is no net force, and thus no net acceleration or change in velocity.

Use the equation  to find the distance traveled in each part of the trip.

Part 1 (east): 

Part 2 (north): 

Part 3 (east): 

Find the total distance traveled in each direction.

Treat these components as sides of a right triangle, in which the hypotenuse represents the total displacement. Find the hypotenuse of this triangle using the Pythagorean theorem.

Now that we have the magnitude of the displacement, we still need to find the directional angle. The angle north of east can be found with an inverse trigonometry function, such as inverse tangent. We know that we are working with a triangle with sides of north and east, and the hypotenuse equal to the displacement. Orienting the angle, we can see that the opposite side is the northwards displacement, and the adjacent side is the eastwards displacement.

The average velocity is equal to displacement over time.

The displacement of the race car is zero because the ending position was the same as the starting position. The average velocity will therefore also be equal to zero. 

Remember that velocity is a vector, while speed is a scalar. Velocity is measured in terms of displacement and speed is measured in terms of distance.

Displacement is a vector quantity, so we cannot simply add the distances. Instead, we will need to triangulate the position of the plane.

We can draw the plane's path on a set of coordinate axes. The initial displacement will be in the vertical direction. The plane will then travel an equivalent distance at an angle of to the horizontal ( to the original flight path), essentially with a slope of one. By bisecting the angle created by the two flight paths, we can create two similar right triangles with hypotenuse lengths of . The measure of the bisected angle will be .

We need to solve for the side opposite the bisected angle, given the length of the hypotenuse. We will use the sine function.

This is the length on only one of the triangle sides. We need to double this distance to find the total displacement.

Since  we need to solve for the total distance around the track. 

Now, we can solve for speed using our equation. With 60 seconds per minute, 3 minutes is equal to 180 seconds.

Keep in mind that the question asked for the average speed, not velocity. Had it asked for the average velocity,  would be the correct answer, as the total displacement is zero.

Keep in mind that velocity is a vector, and a change in direction results in a change in velocity. When a runner runs in a circular manner around a track, the velocity of the runner will oscillate between a maximum positive velocity and a minimum negative velocity. As a result, this scenario matches the velocity vs. time graph appropriately. 

To solve this question, you must understand the difference between total distance and total displacement. While it is true that the baseball traveled a specific distance, the displacement is the final position of the baseball relative to the original position of the ball. The ball started and ended in the same place, so its total displacement is 0m.