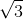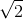In order to solve for , we need to isolate the  to one side of the equation. 

For this problem, the first thing we want to do is distribute the :

Next, we can subtract  from both sides:

Finally, we divide  from both sides:

In order to solve this problem, we need to recall our exponent rules:

When our base numbers are equal to each other, like in this problem, we can add our exponents together using the following formula:

Let's apply this rule to our problem

Solve for the exponents

We cannot leave this problem in this format because we cannot have a negative exponent. Instead, we can move the base and the exponent to the denominator of a fraction:

Solve the problem

There are a couple of ways to solve a system of linear equations: graphically and algebraically. In this lesson, we will review the two ways to solve a system of linear equations algebraically: substitution and elimination. 

Substitution can be used by solving one of the equations for either  or , and then substituting that expression in for the respective variable in the second equation. You could also solve both equations so that they are in the  form, and then set both equations equal to each other. 

Elimination is best used when one of the variables has the same coefficient in both equations, because you can then use addition or subtraction to cancel one of the variables out, and solve for the other variable. 

For this problem, substitution makes the most sense because the first equation is already solved for a variable. We can substitute the expression that is equal to , into the  of our second equation:

Next, we need to distribute and combine like terms:

We are solving for the value of , which means we need to isolate the  to one side of the equation. We can subtract  from both sides:

Then divide both sides by  to solve for 

Remember, when we are solving a system of linear equations, we are looking for the point of intersection; thus, our answer should have both  and  values. 

Now that we have the value of , we can plug that value into the  variable in one of our given equations and solve for 

Our point of intersection, and the solution to the two system of linear equations is 

Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers. 

Rational numbers are numbers that we use most often, and can be written as a simple fraction. 

Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end. 

In this case,  is our only rational number because it can be written as a simple fraction: 

Our answer choices consist of two types of numbers: rational numbers and irrational numbers. In order to correctly answer this question, we need to know the difference between the two types of numbers. 

Rational numbers are numbers that we use most often, and can be written as a simple fraction. 

Irrational numbers cannot be written as fractions, and are numbers that have decimal places that never repeat or end. 

In this case,  is our only irrational number because it cannot be written as a simple fraction.

The first step to solving this problem is to combine like terms:

Next, we can solve our two separate multiplication problems starting with the expression on the left:

In order to solve the next expression, we need to recall our exponent rules from a previous lesson:

When our base numbers are equal to each other, like in this problem, we can add our exponents together using the following formula:

Let's apply this rule to our problem:

The question asked us to leave our answer in scientific notation; thus,  is the correct answer. 

First, let's define the possible transformations. 

Rotation: A rotation means turning an image, shape, line, etc. around a central point.

Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.

Reflection: A reflection mean flipping an image, shape, line, etc. over a central line. 

In the images from the question, notice that the black angle rotates  counterclockwise, or left around the y-axis. The vertical, base, line of the angle goes from being the base, to the top; thus the transformation is a rotation. 

The transformation can't be a reflection over the x-axis because the orange angle didn't flip over the x-axis. 

The transformation can't be a translation because the angle changes direction, which does not happened when you simply move or slide an angle or image. 

A dilation creates an image of the same shape, but of a different size. Dilations are always done with a certain scale factor. Let's look at the image in the picture and determine the length and width of each of the rectangles:

Notice that both the length and the width of the rectangle doubles in the purple rectangle, from the blue rectangle; thus the scale of the dilation is 

In order to solve this problem, we need to recall the formula used to calculate the volume of a cone:

Now that we have this formula, we can substitute in the given values and solve:

The data points in the scatter plot move up the y-axis as the x-axis decreases; thus the data points show a negative association. Also, the data points do not curve, or go up and down, but gradually decreased; thus the scatter plot shows a linear association. We could even draw a "best fit" line: