ISEE Upper Level Quantitative : ISEE Upper Level (grades 9-12) Quantitative Reasoning
Study concepts, example questions & explanations for ISEE Upper Level Quantitative
All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #31 : How To Find The Missing Part Of A List
A geometric sequence begins
What number replaces the circle?
Since this is a geometric sequence, each entry in the sequence is obtained by multiplying the previous entry by the same number - this number is
Now we can find the next three entries in the sequence:
This replaces the square.
Example Question #32 : How To Find The Missing Part Of A List
An arithmetic sequence begins
What number replaces the circle?
Since this is an arithmetic sequence, each entry in the sequence is obtained by adding the same number to the previous entry - this number is
The next three entries in the sequence are computed as follows:
Example Question #33 : How To Find The Missing Part Of A List
A geometric sequence begins
What number replaces the square?
Each term of a geometric sequence is obtained by multiplying the previous one by the same number (common ratio); this number is
Let 
Example Question #32 : How To Find The Missing Part Of A List
The Fibonacci sequence is formed as follows:
For all integers 
Which of the following is true of 
To express 
Also
and
the correct choice.
Example Question #35 : How To Find The Missing Part Of A List
The Fibonacci sequence is defined as follows:
For integers 
Which is the greater quantity?
(a)
(b)
(b) is greater
(a) and (b) are equal
It is impossible to determine which is greater from the information given.
(a) is greater
(a) is greater
The Fibonacci sequence begins as follows:
This sequence is seen to be an increasing sequence. Therefore, each term is greater than its preceding term. In particular,
If we substitute 51 for 
This makes (a) greater.
Example Question #36 : How To Find The Missing Part Of A List
Define a sequence as follows:
For all integers 
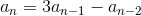
Which of the following expressions is equal to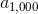 
Setting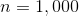 
Similarly,
Substituting:
Example Question #1 : Equations
A company makes toy boats. Their monthly fixed costs are $1500. The variable costs are $50 per boat. They sell boats for $75 a piece. How many boats must be sold each month to break even?
60
100
50
75
60
The break-even point is where the costs equal the revenues
Fixed Costs + Variable Costs = Revenues
1500 + 50x = 75x
Solving for x results in x = 60 boats sold each month to break even.
Example Question #2 : Equations
Sally sells cars for a living. She has a monthly salary of $1,000 and a commission of $500 for each car sold. How much money would she make if she sold seven cars in a month?
$5,000
$4,000
$4,500
$5,500
$4,500
The commission she gets for selling seven cars is $500 * 7 = $3,500 and added to the salary of $1,000 yields $4,500 for the month.
Example Question #2 : How To Find The Solution To An Equation
Solve the following system of equations: x – y = 5 and 2x + y = 4.
What is the sum of x and y?
9
6
5
1
1
Add the two equations to get 3x = 9, so x = 3. Substitute the value of x into one of the equations to find the value of y; therefore x = 3 and y = –2, so their sum is 1.
Example Question #3 : How To Find The Solution To An Equation
If x = 1/3 and y = 1/2, find the value of 2x + 3y.
1
13/6
2
6/5
13/6
Substitute the values of x and y into the given expression:
2(1/3) + 3(1/2)
= 2/3 + 3/2
= 4/6 + 9/6
= 13/6
Certified Tutor
All ISEE Upper Level Quantitative Resources
