All ISEE Upper Level Quantitative Resources
Example Questions
Example Question #82 : Quadrilaterals
A rectangle has length 72 inches and width 36 inches. What is its perimeter?
Each of the other choices is equal to the correct perimeter.
Each of the other choices is equal to the correct perimeter.
The perimeter of a rectangle is equal to twice the sum of its length and its width, which here would be, in inches,

Therefore, the correct choice is that all four measurements are equal to the perimeter.
Example Question #291 : Isee Upper Level (Grades 9 12) Quantitative Reasoning
Which quantity is greater?
(a) The perimeter of a square with area 10,000 square centimeters
(b) The perimeter of a rectangle with area 8,000 square centimeters
(b) is greater
It is impossible to tell from the information given
(a) and (b) are equal
(a) is greater
It is impossible to tell from the information given
A square with area 10,000 square centimeters has sidelength 

Not enough information is given about the rectangle with area 8,000 square centimeters to determine its perimeter. For example, if its dimensions are 100 centimeters by 80 centimeters, its perimeter is 

Example Question #292 : Plane Geometry
Which is the greater quantity?
(a) The perimeter of the rectangle on the coordinate plane with vertices
(b) The perimeter of the rectangle on the coordinate plane with vertices
(b) is greater.
It is impossible to tell from the information given.
(a) is greater.
(a) and (b) are equal.
It is impossible to tell from the information given.
(a) The first rectangle has width 


(b) The second rectangle has width 


For the first rectangle to have a greater perimeter, it is necessary for


We do not know the relative values of 

Example Question #291 : Plane Geometry
A rectangle is two feet longer than it is wide; its perimeter is 11 feet. What is its area in square inches?
It is impossible to determine the area from the information given
The length of the rectangle is 2 feet, or 24 inches, greater than the width, so, if 

The perimeter of the rectangle is 11 feet, or 

The width is 21 inches, and the length is 45 inches. The area is their product:

Example Question #291 : Plane Geometry

Give the perimeter of the above rectangle in terms of 
Opposite sides of a rectangle are of equal length, so the two missing sidelengths are 5 (right) and 
Example Question #294 : Plane Geometry
The sum of the lengths of three sides of a square is one meter. Give the perimeter of the square in millimeters.
A square has four sides of the same length.
The sum of the lengths of three sides of a square is one meter, which is equal to 1,000 millimeters, so each side has length

and the perimeter is four times this, or

Example Question #295 : Plane Geometry
The area of a rectangle is 4,480 square inches. Its width is 70% of its length.
What is its perimeter?
It is impossible to determine the area from the given information.
If the width of the rectangle is 70% of the length, then

The area is the product of the length and width:
The perimeter is therefore

Example Question #296 : Plane Geometry
The area of Rectangle 




The area of the rectangle can be factored as the difference of squares:
The area of a rectangle is the product of its two dimensions, one of which is 
The perimeter is twice the sum of the two dimensions:
Example Question #292 : Geometry

Note: Figure NOT drawn to scale
The above figure shows Rhombus 
Which is the greater quantity?
(a)
(b)
(b) is the greater quantity
(a) is the greater quantity
(a) and (b) are equal
It is impossible to determine which is greater from the information given
(a) and (b) are equal
The opposite sides of a parallelogram - a rhombus included - are congruent, so

Also, Quadrilateral 


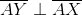


Example Question #292 : Isee Upper Level (Grades 9 12) Quantitative Reasoning

(A) The surface area of a rectangular prism with length 

(B) The surface area of a rectangular prism with length 


It is impossible to determine which is greater from the information given
(B) is greater
(A) is greater
(A) and (B) are equal
(A) is greater
The surface area of a rectangular prism can be determined using the formula:
Using substitutions, the surface areas of the prisms can be found as follows:
The prism in (A):
Regardless of the value of 

Certified Tutor
Certified Tutor
All ISEE Upper Level Quantitative Resources























































![P = 2[(x+9)+(x-9)] = 2(x+x+9-9) = 2(2x)= 4x](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/513707/gif.latex)

















