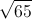All ISEE Upper Level Math Resources
Example Questions
Example Question #44 : Geometry
A right triangle has a hypotenuse of 10 and a side of 6. What is the missing side?
To find the missing side, use the Pythagorean Theorem 



Example Question #1 : Triangles

Refer to the above diagram. Which of the following quadratic equations would yield the value of 
By the Pythagorean Theorem,
Example Question #4 : Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram. Which of the following quadratic equations would yield the value of 
By the Pythagorean Theorem,
Example Question #3 : Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram.
Find the length of 
First, find 
Since 


Example Question #6 : Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram.
Find the length of 
First, find 
Since 


Example Question #3 : Triangles

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 
By the Pythagorean Theorem,
Example Question #8 : Triangles
A right triangle 




Insufficient information is given to answer the question.
The arcs intercepted by a right angle are both semicircles, so hypotenuse 


By the Pythagorean Theorem,
Example Question #1 : How To Find If Right Triangles Are Similar



Which is the greater quantity?
(a)
(b)
(a) is greater.
It is impossible to tell from the information given.
(a) and (b) are equal.
(b) is greater.
(a) and (b) are equal.



The hypotenuse 



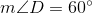

Example Question #51 : Plane Geometry
If a right triangle has a base of 

To solve this problem, we must utilize the Pythagorean Theorom, which states that:
We know that the base is 





Next we evaluate the exponents:
Now we add them together:
Then, 


Example Question #52 : Plane Geometry
If a right triangle has a base of 

To solve this problem, we are going to use the Pythagorean Theorom, which states that 
We know that this particular right triangle has a base of 



Next, we evaluate the expoenents:
Then, 
To solve for 


All ISEE Upper Level Math Resources