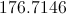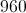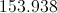If a secant segment and a tangent segment are constructed to a circle from a point outside it, the square of the distance to the circle along the tangent is equal to the product of the distances to the two points on the circle along the secant; in other words,

,

and, substituting, 

Distributing and writing in standard quadratic polynomial form,

We can factor the polynomial by looking for two integers with product  and sum 24; through some trial and error, we find that these numbers are 32 and , so we can write this as 

By the Zero Product Principle, 

, in which case  - impossible since  is a (positive) distance; or,

, in which case  - the correct choice.

If two chords of a circle intersect inside the circle, the product of the lengths of the parts of each chord is the same. In other words,

Solving for :

Simplifying the radical using the Product of Radicals Principle, and noting that the greatest perfect square factor of 96 is 16:

If a secant segment line and a tangent segment are constructed to a circle from a point outside it, the square of the length of the tangent is equal to the product of the distances to the two points on the circle intersected by the secant; in other words,

Substituting:

Distributing, then solving for :

The circumference of a circle can be found using the following equation:

The equation for finding the area of a circle is . 

Therefore, the equation for finding the value of the radius in the circle with an area of  is:

The circumference of a circle can be found using the following equation:

We plug in the circumference given,  into  and use algebraic operations to solve for .

Inscribed , which measures , intercepts a minor arc with twice its measure. That arc is , which consequently has measure 

.

The corresponding major arc, , has as its measure

, and is

of the circle.

If we let  be the circumference and  be the radius, then  has length

.

This is equal to , so we can solve for  in the equation

The radius of the circle is 50.

A circle has a circumference of . What is the radius of the circle?

Begin with the formula for circumference of a circle:

Now, plug in our known and work backwards:

Divide both sides by two pi to get:

You are exploring the woods near your house, when you come across an impact crater. It is perfectly circular, and you estimate its area to be .

What is the radius of the crater?

To solve this, we need to recall the formula for the area of a circle.

Now, we know A, so we just need to plug in and solve for r!

Begin by dividing out the pi

Then, square root both sides.

So our answer is 13m.

The formula for finding the area of a circle is . In this formula, represents the radius of the circle.  Since the question only gives us the measurement of the diameter of the circle, we must calculate the radius.  In order to do this, we divide the diameter by .

Now we use for in our equation.