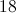All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #132 : Statistics & Probability
Given the following data sets of data, identify how the median would change if an additional data point of 
Data Set:
New Data Set:
First, we need to find the median for the first data set:
We must put the numbers in order from least to greatest:
Since there is an even number of items in the data set, we will take the average of the middle two numbers to find the median.
The median for this data set is:

Next, we must find the new median for the new data set:
Again, we must put the numbers in order from least to greatest:
Since there is an odd number of items, we can choose the middle number to be the median.
In this case, the middle number is 
Therefore, we know that the median will decrease by 
Example Question #342 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
Horatio's soccer team has scored the below number of goals in their last eight games, what is the median number of goals that have been scored?
First we must put the numbers 
After the numbers are in order, if it is an odd number of numbers we chose the middle number - that is the median.
In this case, we have an even number of numbers, so we must take the average of the middle two numbers which is given below:
So the median is 
Example Question #11 : Median
Horatio's soccer team has scored the below number of goals in their last 
Horatio calculates the median to be 



The median will increase by
The median will remain unchanged
The median will increase by
The median will increase by
The median will remain unchanged
When finding the median we must first reorganize the numbers from least to greatest, here is what the numbers are before and after they were organized.
Given:
After Organized from least to greatest:
In order to find the Median for an even number of numbers (we have 
Here we would add 


If we were to change the 




The middle two numbers are still 

The Median will remain unchanged.
Example Question #15 : Find Median
Find the median of the data set provided:

In order to answer this question correctly, we need to recall the definition of median:
Median: The median of a data set is the middle value, when the data set is ordered from least to greatest.
In order to find the median, we need to first organize the data from least to greatest:
Next, we can solve for the median by finding the middlemost number in our data:
The median for this data set is
Example Question #16 : Find Median
Find the median of the data set provided:

In order to answer this question correctly, we need to recall the definition of median:
Median: The median of a data set is the middle value, when the data set is ordered from least to greatest.
In order to find the median, we need to first organize the data from least to greatest:
Next, we can solve for the median by finding the middlemost number in our data:
The median for this data set is
Example Question #17 : Find Median
Find the median of the data set provided:

In order to answer this question correctly, we need to recall the definition of median:
Median: The median of a data set is the middle value, when the data set is ordered from least to greatest.
In order to find the median, we need to first organize the data from least to greatest:
Next, we can solve for the median by finding the middlemost number in our data:
The median for this data set is
Example Question #18 : Find Median
Find the median of the data set provided:

In order to answer this question correctly, we need to recall the definition of median:
Median: The median of a data set is the middle value, when the data set is ordered from least to greatest.
In order to find the median, we need to first organize the data from least to greatest:
Next, we can solve for the median by finding the middlemost number in our data:
The median for this data set is
Example Question #1 : How To Find The Answer From A Table
Choose the best answer from the four choices given.
Katie wants to buy as many umbrellas as she can to give to her friends as Christmas gifts. She finds a deal online where she can get umbrellas for $7 each or four umbrellas for $25 (including tax). If shipping is $3 for every $20 of merchandise (or portion thereof), how many umbrellas can she buy if she has $140?
The quickest way to solve this problem is by making a chart showing the units purchased and the total cost. Start with the 4-packs of umbrellas:
4-packs cost shipping cost total cost
1 $25 $6 $31
2 $50 $9 $59
3 $75 $12 $87
4 $100 $15 $115
5 $125 $21 $146 (too high)
Having determined that Katie can buy four of the 4-packs of umbrellas, now we see how many of the $7 individual umbrellas she can add to her order.
four 4-packs indiv. indiv. $ subtotal shipping $ total $
$100 1 $7 $107 $18 $125
$100 2 $14 $114 $18 $132
$100 3 $21 $121 $21 $142 (too high)
Therefore, Katie can buy (4) 4-packs and (2) individual umbrellas (18 total umbrellas) for $132.
ALTERNATIVELY, you can begin by determining the highest subtotal she can afford and work backwards from there. $120 is 6 x $20, so the shipping charge would be $6 x 3 = $18, for a total cost of $138. One more dollar on the subtotal would bring it into the next $20 segment, bringing the shipping charge up to $21 (and $142 is greater than $140). Thus, from here you could figure out the maximum number of $25 4-packs and $7 individual umbrellas Katie could buy with $120.
Since $6 is not enough to buy any umbrellas, the total would be
Example Question #1 : Tables
The table below gives the population of Buchanan City in each census year from 1930 to 1980.
Which is the greater quantity?
(a) The decline in the population of Buchanan City between 1940 and 1950
(b) The growth in the population of Buchanan City between 1950 and 1960
It is impossible to tell from the information given
(b) is greater
(a) and (b) are equal
(a) is greater
(b) is greater
The population of Buchanan City in 1960 is greater than it was in 1940, so its decline between 1940 and 1950 must be less than its growth between 1950 and 1960.
Example Question #2 : Tables
The table below gives the population of Buchanan City in each census year from 1930 to 1980.
Which is the greater quantity?
(a) The growth in the population of Buchanan City between 1930 and 1940
(b) The growth in the population of Buchanan City between 1950 and 1960
(a) is greater
It is impossible to tell from the information given
(b) is greater
(a) and (b) are equal
(b) is greater
(a) Between 1930 and 1940, the population grew by
(b) Between 1950 and 1960, the population grew by 
This makes (b) greater
Certified Tutor
Certified Tutor
All ISEE Middle Level Quantitative Resources