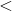All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #11 : Prime Numbers
Which of the following is the product of two distinct prime numbers?
There are two key terms in this question that we need to understand in order to answer the question correctly: product and prime numbers.
Product is the answer to a multiplication problem.
Prime numbers are numbers that are greater than and only have factors of the number
and itself. For example
is a prime number because it's greater than
and the factors of
are only
and
.
To find the correct answer, we need to know the factor pairs for our answer choices. The correct answer will have a factor pair of two prime numbers.
Let's look at our answer options:
- A factor pair for
is
, and













and


Example Question #12 : Prime Numbers
Which of the following is the product of two distinct prime numbers?
There are two key terms in this question that we need to understand in order to answer the question correctly: product and prime numbers.
Product is the answer to a multiplication problem.
Prime numbers are numbers that are greater than and only have factors of the number
and itself. For example
is a prime number because it's greater than
and the factors of
are only
and
.
To find the correct answer, we need to know the factor pairs for our answer choices. The correct answer will have a factor pair of two prime numbers.
Let's look at our answer options:
- A factor pair for
is
, and
is not a prime number.
- A factor pair for
is
, and
is not a prime number.
- A factor pair for
is
, and
is not a prime number.




are prime numbers, thus

Example Question #11 : Prime Numbers
Which of the following is the product of two distinct prime numbers?
There are two key terms in this question that we need to understand in order to answer the question correctly: product and prime numbers.
Product is the answer to a multiplication problem.
Prime numbers are numbers that are greater than and only have factors of the number
and itself. For example
is a prime number because it's greater than
and the factors of
are only
and
.
To find the correct answer, we need to know the factor pairs for our answer choices. The correct answer will have a factor pair of two prime numbers.
Let's look at our answer options:
- A factor pair for
is
, and
is not a prime number.











and


Example Question #382 : Number Concepts And Operations
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #321 : Fractions
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #2 : Compare Two Fractions With Different Numerators And Different Denominators: Ccss.Math.Content.4.Nf.A.2
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #23 : Extend Understanding Of Fraction Equivalence And Ordering
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #391 : Number Concepts And Operations
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #1461 : Ssat Upper Level Quantitative (Math)
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Example Question #4 : Compare Two Fractions With Different Numerators And Different Denominators: Ccss.Math.Content.4.Nf.A.2
Select the symbol to correctly fill in the blank below.

To compare fractions, we need to first make common denominators.
Now that we have common denominators, we can compare numerators. The fraction with the bigger numerator has the greater value.
Certified Tutor
Certified Tutor
All ISEE Lower Level Quantitative Resources