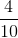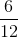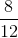All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #41 : Quadrilaterals
What is the area of a parallelogram with a height of 

The formula for finding the area of a parallelogram is the same as that of finding the area of a rectangle:
In this case, the area equals 


Example Question #41 : Quadrilaterals
Ted drew the parallelogram shown below.

What is the area of the parallelogram?
26 square feet
160 square feet
32 square feet
40 square feet
20 square feet
32 square feet
The area of a parallelogram can be found by multiplying the base times the height. The height is the perpendicular distance between two bases. In the above parallelogram, the base is 8 and its height is 4, giving the equation 8 x 4 = A. The area is 32 square feet.
Example Question #1 : How To Find The Area Of A Parallelogram
Wilhelmina drew the parallelogram below.

What is the area of the parallelogram?
40 square millimeters
72 square millimeters
80 square millimeters
42 square millimeters
96 square millimeters
72 square millimeters
The area of a parallelogram can be found by multiplying the base times the height. The height is the perpendicular distance between two bases. In the above parallelogram, the base is 12 and its height is 6, giving the equation 12 x 6 = A. The area is 72 square millimeters.
Example Question #1 : How To Find The Area Of A Parallelogram
Find the area of the following parallelogram.

In order to find the area of a parallelogram we use the equation
In this case our values are
So, our area is:
Example Question #1 : How To Find The Area Of A Parallelogram
Find the area of the following parallelogram.

The equation for the area of a parallelogram is 
In this case, our values are
so, the area is:
Example Question #123 : Quadrilaterals
What area of the rectangle is filled in?

Area is the amount of space within the perimeter of a two-dimensional shape. The rectangle is split into 


Example Question #271 : Geometry
What area of the rectangle is filled in?

Area is the amount of space within the perimeter of a two-dimensional shape. The rectangle is split into 


Example Question #1 : How To Find The Area Of A Parallelogram
What area of the rectangle is filled in?

Area is the amount of space within the perimeter of a two-dimensional shape. The rectangle is split into 


Example Question #124 : Quadrilaterals
What area of the rectangle is filled in?

Area is the amount of space within the perimeter of a two-dimensional shape. The rectangle is split into 


Example Question #22 : Geometry
What area of the rectangle is filled in?

Area is the amount of space within the perimeter of a two-dimensional shape. The rectangle is split into 


All ISEE Lower Level Quantitative Resources